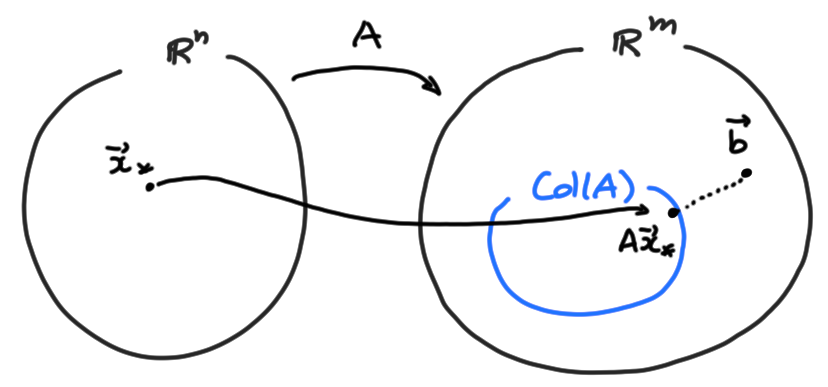
Considérons un système de taille \(m\times n\), \[ (*):\quad A\boldsymbol{x}=\boldsymbol{b}\,, \] que l'on supposera incompatible, ce qui signifie \[ \min_{\boldsymbol{x}\in \mathbb{R}^n} \|A\boldsymbol{x}-\boldsymbol{b}\|\gt 0\,. \]
Schématiquement:
Remarque: À propos de la terminologie ''moindres carrés'', trouver le \(\boldsymbol{x}\) qui minimise une certaine norme revient au même que de trouver le \(\boldsymbol{x}\) qui minimise le carré de cette norme , donc la recherche d'une pseudo-solution revient à minimiser la fonction \[ \boldsymbol{x}\mapsto \|A\boldsymbol{x}-\boldsymbol{b}\|^2=\sum_{k=1}^m\bigl((A\boldsymbol{x})_k-b_k\bigr)^2\,, \] qui est une somme de carrés.
On présente de façon explicite les arguments indiqués dans la section précédente.
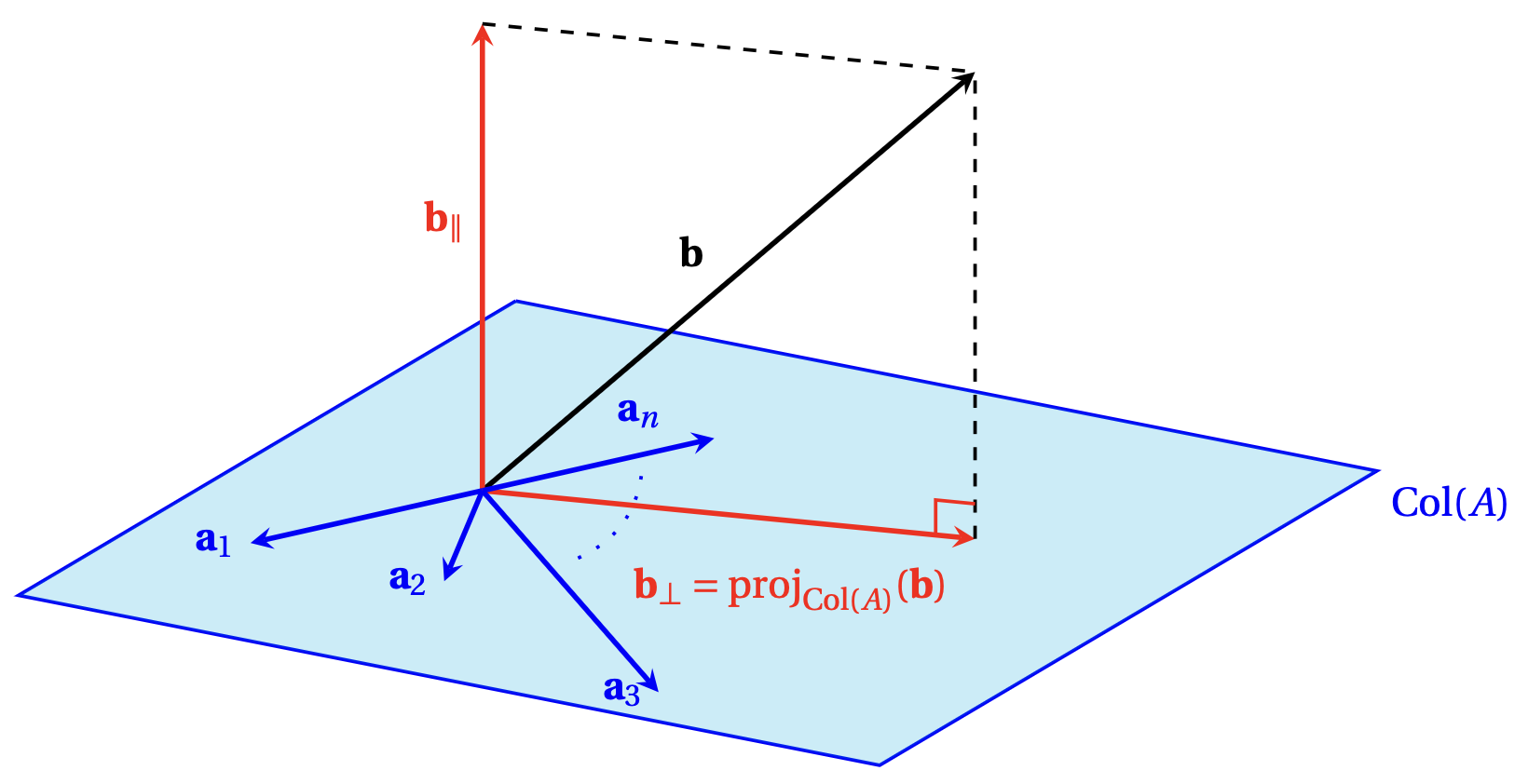
Par la dernière propriété de la projection orthogonale dans le Théorème de la Section (cliquer), on sait que \[ \|\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})-\boldsymbol{b}\|= \min_{\boldsymbol{x}\in \mathbb{R}^n} \|A\boldsymbol{x}-\boldsymbol{b}\|\,, \] ce qui nous dit que toute préimage \(\hat{\boldsymbol{x}}\in\mathbb{R}^n\) de \(\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\) par \(A\) est solution de \(A\boldsymbol{x}=\boldsymbol{b}\) au sens des moindres carrés. De façon réciproque, si \(\hat{\boldsymbol{x}}\in\mathbb{R}^n\) est solution de \(A\boldsymbol{x}=\boldsymbol{b}\) au sens des moindres carrés, alors \[ \|A\hat{\boldsymbol{x}}-\boldsymbol{b}\|= \min_{\boldsymbol{x}\in \mathbb{R}^n} \|A\boldsymbol{x}-\boldsymbol{b}\|\,. \] Comme \(A\hat{\boldsymbol{x}}\) est dans \(\mathrm{Col}(A)\), la dernière propriété de la projection orthogonale dans le le Théorème de la Section (cliquer) nous dit que \(A\hat{\boldsymbol{x}} = \mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\), comme on voulait démontrer.
Considérons une pseudo-solution \(\hat{\boldsymbol{x}}\):
\[ \|A\hat{\boldsymbol{x}}-\boldsymbol{b}\|=
\min_{\boldsymbol{x}\in \mathbb{R}^n} \|A\boldsymbol{x}-\boldsymbol{b}\|\,.
\]
Comme on sait, considérer tous les produits \(\boldsymbol{q}:=
A\boldsymbol{x}\) possibles, lorsque
\(\boldsymbol{x}\) varie, revient à considérer toutes les combinaisons linéaires
possibles des colonnes de \(A\), et donc à parcourir tout le sous-espace
\(\mathrm{Col}(A)\). Donc on peut tout aussi bien écrire
\[
\min_{\boldsymbol{x}\in \mathbb{R}^n} \|A\boldsymbol{x}-\boldsymbol{b}\|=
\min_{\boldsymbol{q}\in \mathrm{Col}(A)} \|\boldsymbol{q}-\boldsymbol{b}\|\,.
\]
Or on a vu que le minimum de cette distance est réalisé lorsque \(\boldsymbol{q}\) est
la projection de \(\boldsymbol{b}\) sur \(\mathrm{Col}(A)\):
\[
\hat{\boldsymbol{q}}
=\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})
\]
On peut toujours calculer cette projection, typiquement en extrayant une
base de \(\mathrm{Col}(A)\), et en l'orthogonalisant avec le procédé de Gram-Schmidt.
(C'est ce que nous avons fait dans l'exemple de l'introduction.)
Mais nous allons voir qu'il est possible de passer outre le calcul explicite de
cette projection.
Théorème: Un vecteur \(\hat{\boldsymbol{x}}\in\mathbb{R}^n\) est solution de \(A\boldsymbol{x}=\boldsymbol{b}\) au sens des moindres carrés si et seulement si \(\hat{\boldsymbol{x}}\) est solution de l'équation normale, donnée par \[ A^TA\boldsymbol{x}=A^T\boldsymbol{b}\,. \]
Si \(\hat{\boldsymbol{x}}\in\mathbb{R}^n\) est solution de \(A\boldsymbol{x}=\boldsymbol{b}\) au sens des moindres carrés, alors le premier théorème de cette section nous dit que \(A\boldsymbol{x}=\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\). Or, on rappelle que \(\boldsymbol{b}_\parallel=\mathrm{proj}_{\mathrm{Col}(A)}(\boldsymbol{b})\) est caractérisé par le fait que \(\boldsymbol{b}_\perp:= \boldsymbol{b}-\boldsymbol{b}_\parallel\) est orthogonal à \(\mathrm{Col}(A)\), i.e. \(\boldsymbol{b}_\perp\in \mathrm{Col}(A)^\perp\):
Exemple: Considérons l'exemple de l'introduction, où le système incompatible \(A\boldsymbol{x}=\boldsymbol{b}\) de départ était \[ \begin{pmatrix} 2&1\\ 12&1\\ 65&1 \end{pmatrix} \begin{pmatrix} \alpha\\ \beta \end{pmatrix} = \begin{pmatrix} 30\\52 \\147 \end{pmatrix}\,. \] Donnons la solution de cette équation sans passer par la projection, en utilisant le théorème ci-dessus. On obtient l'équation normale en multipliant des deux côtés par \(A^T\), qui donne \[ \begin{pmatrix} 2&12&65\\ 1&1&1 \end{pmatrix} \begin{pmatrix} 2&1\\ 12&1\\ 65&1 \end{pmatrix} \begin{pmatrix} \alpha\\ \beta \end{pmatrix} = \begin{pmatrix} 2&12&65\\ 1&1&1 \end{pmatrix} \begin{pmatrix} 30\\52 \\147 \end{pmatrix}\,, \] c'est-à-dire \[ \begin{pmatrix} 4373&79\\ 79&3 \end{pmatrix} \begin{pmatrix} \alpha\\ \beta \end{pmatrix} = \begin{pmatrix} 10239\\229 \end{pmatrix}\,. \] La solution de ce dernier est donnée par \[\begin{aligned} \alpha&=\frac{12626}{6878}=1.8357\dots\,, \\ \beta&=\frac{192536}{6878}=27.9930\dots\,, \end{aligned}\] comme nous avions trouvé en utilisant la projection.
Dans l'exemple précédent, la solution de l'équation normale était unique. Mais il peut arriver que l'équation normale possède plus d'une solution, ce que l'on aimerait éviter dans les problèmes pratiques. Voyons comment garantir l'unicité de la pseudo-solution:
Théorème: Soit \(A\) une matrice de taille \(m\times n\). Les condition suivantes sont équivalents:
Ainsi, lorsque la pseudo-solution \(\hat{\boldsymbol{x}}\) du système \(A\boldsymbol{x}=\boldsymbol{b}\) est unique, elle s'exprime explicitement par \[ \hat{\boldsymbol{x}} =(A^TA)^{-1}A^T\boldsymbol{b}\,. \] Pour la preuve des équivalences énoncées dans le théorème, nous aurons besoin du résultat préliminaire suivant:
Lemme: Pour toute matrice \(A\) de taille \(m\times n\), \(A\boldsymbol{x}=\boldsymbol{0}\) si et seulement si \(A^TA\boldsymbol{x}=\boldsymbol{0}\).
Il est évident que si \(A\boldsymbol{x}=\boldsymbol{0}\), alors
\(A^TA\boldsymbol{x}=\boldsymbol{0}\).
Inversément, si \(A^TA\boldsymbol{x}=\boldsymbol{0}\), alors
\[
\|A\boldsymbol{x}\|^2
=(A\boldsymbol{x})^T(A\boldsymbol{x})
=\boldsymbol{x}^T(A^TA\boldsymbol{x})
=\boldsymbol{0}\,,
\]
ce qui implique \(\|A\boldsymbol{x}\|=0\), c'est-à-dire \(A\boldsymbol{x}=\boldsymbol{0}\).
Passons maintenant à la preuve du théorème:
L'équivalence
(i) \(\Leftrightarrow\)
(ii)
est claire par ce que nous avons montré ci-dessus (un
\(\boldsymbol{x}\) est pseudo-solution si et seulement si c'est une solution de
l'équation normale).
Pour montrer l'équivalence
(ii) \(\Leftrightarrow\)
(iii),
il suffit de noter qu'un système carré \(M\boldsymbol{x}=\boldsymbol{y}\) possède une
unique solution pour tout \(\boldsymbol{y}\) si et seulement si \(M\) est inversible.
Finalement, on va montrer l'équivalence
(iii) \(\Leftrightarrow\)
(iv).
En effet, les colonnes de \(A\) sont indépendantes si et seulement si
l'équation \(A\boldsymbol{x}=\boldsymbol{0}\) ne possède que la solution triviale, et par le
lemme ci-dessus, ceci est équivalent à dire que \(A^TA\boldsymbol{x}=\boldsymbol{0}\) ne
possède que la solution triviale, qui encore une fois
est équivalent à dire que \(A^TA\) est
inversible, qui est la condition
(iii).
Exemple: Le système incompatible \[ \begin{pmatrix} 1&2&3\\ 1&-3&-2\\ 0&5&5\\ -1&1&0 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 1\\ 2\\ 3\\ 4 \end{pmatrix} \] possède une infinité de pseudo-solutions. En effet, la troisième colonne de \(A\) est égale à la somme des deux premières; par le théorème, ceci implique que la solution n'est pas unique. On conclut que le nombre de solutions est infini, par le Théorème ''\(0,1,\infty\)'' appliqué à \(A^TA\boldsymbol{x}=A^T\boldsymbol{b}\).
Plus tard, nous appliquerons la méthode des moindres carrés pour résoudre d'autres problèmes d'optimisation, inspirés de l'analyse.
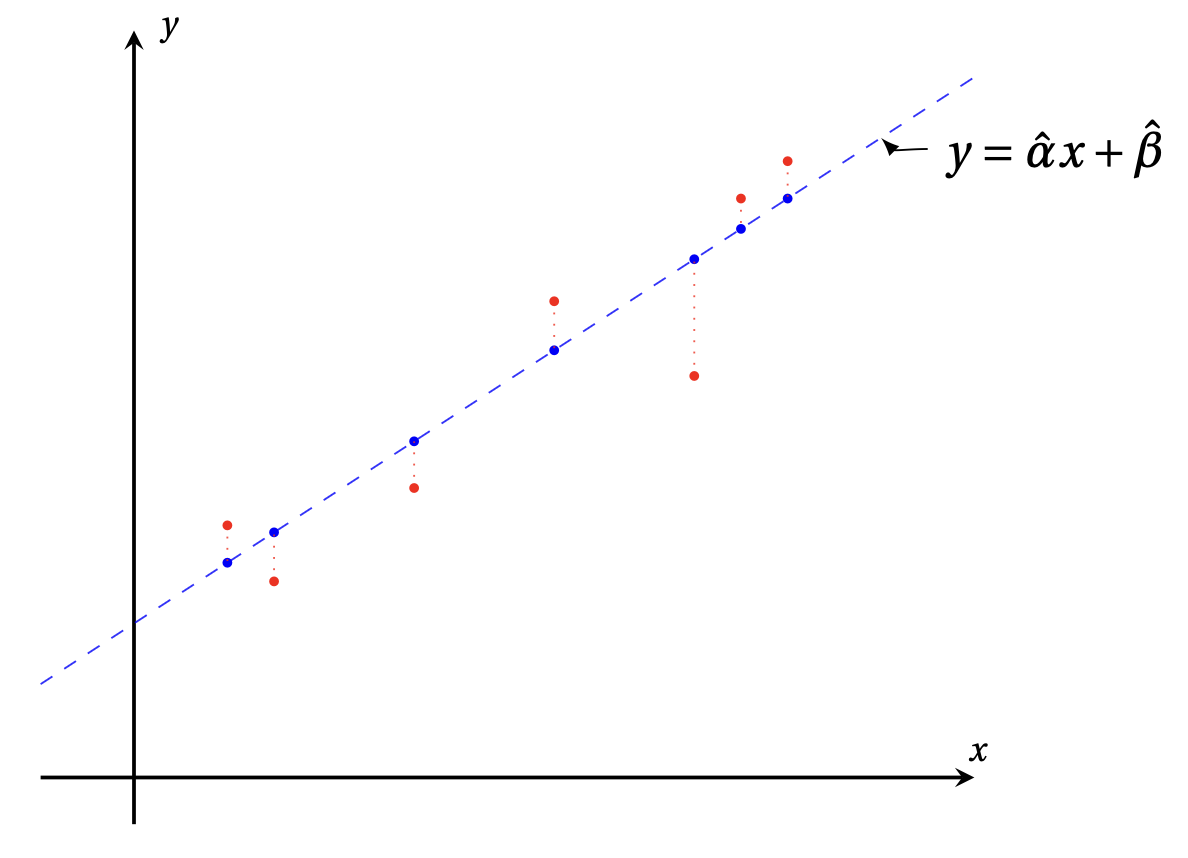
Par exemple, avec seulement \(N=3\) comme dans l'exemple de motivation (faites bouger les points!):
Exemple: On considère la famille \(\mathcal{P}=\{(-6,-1),(-2,2),(1,1),(7,6)\}\) de points du plan. La droite de régression \(y = \hat{\alpha} x + \hat{\beta}\) associée est obtenue à partir de la solution de moindres carrées de \[ \begin{pmatrix} -6 & 1 \\ -2 & 1 \\ 1 & 1 \\ 7 & 1 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} -1 \\ 2 \\ 1 \\ 6 \end{pmatrix}\,. \] Si l'on utilise l'équation normale, on cherche donc à résoudre \[ \begin{pmatrix} 90 & 0 \\ 0 & 4 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} -6 & -2 & 1 & 7 \\ 1 & 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} -6 & 1 \\ -2 & 1 \\ 1 & 1 \\ 7 & 1 \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} -6 & -2 & 1 & 7 \\ 1 & 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} -1 \\ 2 \\ 1 \\ 6 \end{pmatrix} = \begin{pmatrix} 45 \\ 8 \end{pmatrix}\,, \] qui admet la solution unique \[ \begin{pmatrix} \hat{\alpha} \\ \hat{\beta} \end{pmatrix} = \begin{pmatrix} 1/2 \\ 2 \end{pmatrix}\,. \] En conséquence, la droite de régression est \(y = \frac{1}{2}x + 2\).
Dernière compilation: 2025-09-02 (09:33:31)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
