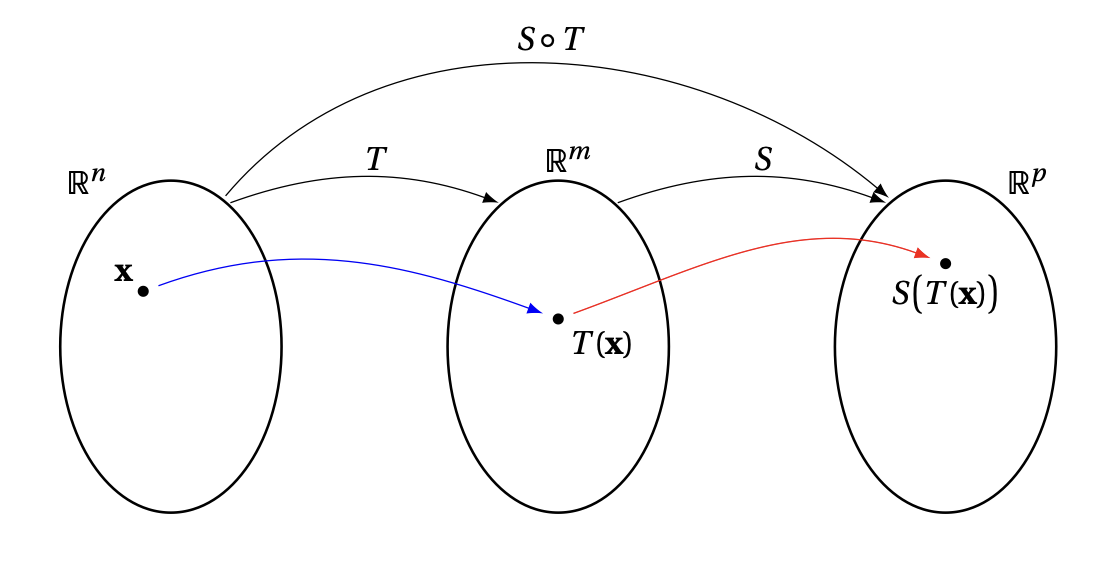
Algèbre linéaire | S. Friedli, S. Herscovich (EPFL)

5.2 Produit matriciel

Le produit de deux matrices est motivé par la composition d'applications linéaires.

Or lorsqu'on veut composer deux applications, il faut que les ensembles qui apparaissent dans leurs définitions soient compatibles.

Soit donc \[T:\mathbb{R}^n\to\mathbb{R}^m\] une application linéaire, dont la matrice de taille \(m\times n\) est notée \(A\). Si \(\boldsymbol{x}\in \mathbb{R}^n\), la \(k\)-ème composante (\(1\leqslant k\leqslant m\)) de \(T(\boldsymbol{x})\) est donnée par \[ \big(T(\boldsymbol{x})\big)_k=(A\boldsymbol{x})_k=\sum_{j=1}^n A_{k,j}x_j\,. \]
Soit ensuite \[S:\mathbb{R}^m\to\mathbb{R}^p\] une autre application linéaire, dont la matrice de taille \(p\times m\) est notée \(B\). Si \(\boldsymbol{x}\in \mathbb{R}^m\), la \(k\)-ème composante (\(1\leqslant k\leqslant p\)) de \(S(\boldsymbol{x})\) est donnée par \[ \big(S(\boldsymbol{x})\big)_k=(B\boldsymbol{x})_k=\sum_{j=1}^m B_{k,j}x_j\,. \]

Puisque l'ensemble d'arrivée de \(T\) est l'ensemble de départ de \(S\), on peut les composer:

On rappelle que la composition est définie par \[\begin{aligned} S\circ T:\mathbb{R}^n&\to \mathbb{R}^p \\ \boldsymbol{x}&\mapsto (S\circ T)(\boldsymbol{x}):= S\big(T(\boldsymbol{x})\big)\,. \end{aligned}\]

Comme on a vu dans le deuxième Lemme %(cliquer) dans la Section (cliquer), la composée \(S\circ T\) est linéaire; elle peut donc être représentée par une matrice. Quelle est cette matrice?

Calculons la \(k\)-ème composante de \((S\circ T)(\boldsymbol{x})\): \[\begin{aligned} (S\circ T)(\boldsymbol{x})_k =\Big(S\big(T(\boldsymbol{x})\big)\Big)_k &=\big(B(A\boldsymbol{x})\big)_k\\ &=\sum_{j=1}^m B_{k,j}(A\boldsymbol{x})_j\\ &={\color{red}\sum_{j=1}^m}B_{k,j}{\color{blue}\sum_{\ell=1}^n}A_{j,\ell}x_\ell\\ &={\color{blue}\sum_{\ell=1}^n} \Bigl( \underbrace{{\color{red}\sum_{j=1}^m}B_{k,j}A_{j,\ell}}_{=:C_{k,\ell}} \Bigr)x_\ell\,. \end{aligned}\] On voit qu'après avoir interverti les sommes sur \(j\) et \(l\), on a pu définir des coefficients \(C_{k,\ell}\), qui sont les coefficients d'une matrice de taille \(p\times n\), notée \(C\), qui permet d'écrire \[ (S\circ T)(\boldsymbol{x})_k =\sum_{\ell=1}^n C_{k,\ell}x_\ell =(C\boldsymbol{x})_k\,. \] On a donc trouvé la matrice associée à \(S\circ T\), et on sait calculer ses coefficients en fonction de ceux de \(A\) et \(B\).

Soient \(B=(B_{i,j})\) une matrice de taille \(p\times m\), et \(A=(A_{i,j})\) une matrice de taille \(m\times n\). Le produit matriciel de \(B\) par \(A\) est la matrice de taille \(p\times n\), notée \(C=B.A\) ou \(C=BA\), dont les coefficients sont définis par \[ C_{k,\ell}:= \sum_{j=1}^m B_{k,j}A_{j,\ell}\,. \] De façon équivalente, si l'on représente \(A\) par ses colonnes via \(A = [\boldsymbol{a}_1 \cdots \boldsymbol{a}_n]\), où \(\boldsymbol{a}_1, \dots, \boldsymbol{a}_n \in \mathbb{R}^m\), alors \[ C = BA = [\underset{\in \mathbb{R}^p}{\underbrace{B\boldsymbol{a}_1}} \cdots \underset{\in \mathbb{R}^p}{\underbrace{B\boldsymbol{a}_n}}]\,. \]

L'expression ci-dessus pour le coefficient \(c_{kl}\) montre que ce dernier se calcule en parcourant la \(k\)-ème ligne de \(A\) et la \(l\)-ème colonne de \(B\).

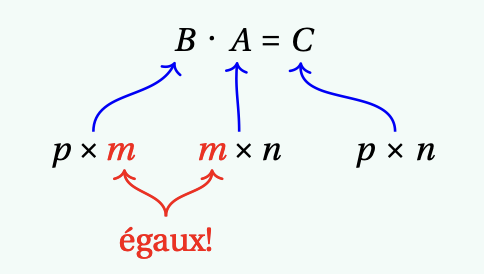
Point clé: la composition d'applications linéaires correspond au produit de matrices
La définition précédente du produit matriciel nous dit que, pour des applications linéaires \( T : \mathbb{R}^n \rightarrow \mathbb{R}^m \) et \( S : \mathbb{R}^m \rightarrow \mathbb{R}^p \), \[ [S \circ T] = [S] \, [T]\,. \]

Exemple: Calculons un produit \(BA=C\), pour des matrices \(4\times 4\): \[ \underbrace{ \begin{pmatrix} 1&2&-2&0\\ {\color{red}3}&{\color{red}2}&{\color{red}-2}&{\color{red}1}\\ -1&1&0&1\\ 5&2&-1&6 \end{pmatrix}}_{B} \underbrace{ \begin{pmatrix} 0&2&{\color{blue}-1}&5\\ 3&1&{\color{blue}5}&-3\\ 2&2&{\color{blue}-1}&1\\ 0&7&{\color{blue}1}&2 \end{pmatrix}}_{A} = \underbrace{ \begin{pmatrix} 2&0&11&-3\\ 2&11&\mathbf{10}&9\\ 3&6&7&-6\\ 4&52&12&30 \end{pmatrix} }_{C}\,. \] Comme exemple, on a indiqué le calcul de \[\begin{aligned} C_{2,3}&=\sum_{j=1}^4 B_{2,j} A_{j,3} \\ &= B_{2,1} A_{1,3} + B_{2,2}A_{2,3} + B_{2,3}A_{3,3} + B_{2,4}A_{4,3}\\ &={\color{red}3}\cdot{\color{blue}(-1)} +{\color{red}2}\cdot{\color{blue}5} +{\color{red}(-2)}\cdot{\color{blue}(-1)} +{\color{red}1}\cdot {\color{blue}1}=\mathbf{10}\,. \end{aligned}\]

On peut multiplier deux matrices de tailles différentes, \(BA\), mais ces tailles doivent être compatibles. Plus précisément, le nombre de colonnes de \(B\) doit être égal au nombre de lignes de \(A\):

Exemple: Le produit d'une matrice de taille \(3\times 2\) par une matrice de taille \(2\times 4\) est bien défini: \[ \underbrace{ \begin{pmatrix} a&b\\ c&d\\ e&f \end{pmatrix} }_{3\times 2} \underbrace{ \begin{pmatrix} 1&2&3&4\\ 5&6&7&8 \end{pmatrix} }_{2\times 4} = \underbrace{ \begin{pmatrix} a+5b&2a+6b&3a+7b&4a+8b\\ c+5d&2c+6d&3c+7d&4c+8d\\ e+5f&2e+6f&3e+7f&4e+8f \end{pmatrix} }_{3\times 4}\,. \] Par contre, dans l'ordre inverse, le produit \[ \underbrace{ \begin{pmatrix} 1&2&3&4\\ 5&6&7&8 \end{pmatrix} }_{2\times 4} \underbrace{ \begin{pmatrix} a&b\\ c&d\\ e&f \end{pmatrix} }_{3\times 2} \qquad \text{n'est pas défini!} \]

Quelques remarques:

Un vecteur \(\boldsymbol{x}\in \mathbb{R}^n\) peut s'interpréter comme une matrice de taille \(n\times 1\). Donc la multiplication d'une matrice de taille \(m\times n\) par \(\boldsymbol{x}\in \mathbb{R}^n\), peut s'interpréter comme le produit matriciel d'une matrie de taille \(m\times n\) par une matrice de taille \(n\times 1\), qui donne une \(A\boldsymbol{x}\) qui est una matrice de taille \(m\times 1\), c'est-à-dire un vecteur de \(\mathbb{R}^m\).
Pour le produit d'une matrice de taille \(1\times n\) par une matrice de taille \(n\times 1\), on obtient une matrice de taille \(1\times 1\), qui n'est autre qu'un réel: \[ \underbrace{ \begin{pmatrix} x_1&x_2&\dots&x_n \end{pmatrix}}_{1\times n} \underbrace{ \begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{pmatrix}}_{n\times 1} =\underbrace{x_1y_1+\cdots+x_ny_n}_{\in \mathbb{R}}\,. \]
Par contre, le produit d'une matrice de taille \(m\times 1\) par une matrice de taille \(1\times n\) donne évidemment une matrice de taille \(m\times n\). Par exemple, \[ \begin{pmatrix} a\\ b\\ c \end{pmatrix} \begin{pmatrix} x&y&z&t \end{pmatrix} = \begin{pmatrix} ax&ay&az&at\\ bx&by&bz&bt\\ cx&cy&cz&ct \end{pmatrix}\,. \]
Considérons le produit de la matrice \(A\) de taille \(m\times n\) par la matrice \(B\) de taille \(n\times p\). Si l'on exprime \(B\) à l'aide de ses \(p\) colonnes, qui sont des vecteurs de \(\mathbb{R}^n\) \[ B=[\boldsymbol{b}_1\cdots \boldsymbol{b}_p]\,, \] alors le produit \(AB\) peut s'écrire à l'aide de ses \(p\) colonnes: \[ AB=[A\boldsymbol{b}_1\cdots A\boldsymbol{b}_p]\,, \] où chaque colonne \(A\boldsymbol{b}_k\in \mathbb{R}^m\)