17.1 Introduction

(CHAPITRE EN COURS DE RÉDACTION)

Dans ce chapitre, nous allons voir une application de l'algèbre linéaire à une notion rencontrée en théorie des probabilités, à savoir les chaînes de Markov.

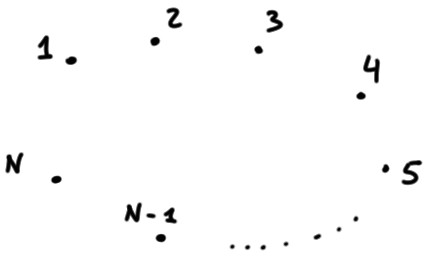
Une chaîne de Markov est une certaine modélisation d'un phénomène aléatoire qui évolue au cours du temps. Pour commencer, considérons un ensemble de \(N\) points, que l'on suppose indexés par un ensemble \[ \chi=\{1,2,3,\dots,N\}\,. \] On peut se représenter cet ensemble comme des indices représentant l'ensemble des états possibles d'un système.

Exemple: Considérons un gaz contenu dans un enceinte hermétique de volume et température variable. L'état thermodynamique du système peut être soit gazeux, liquide ou solide. Dans ce cas on peut utiliser \(\chi=\{1,2,3\}\), où \[ 1=''\text{gazeux}''\,,\qquad 2=''\text{liquide}''\,,\qquad 3=''\text{solide}''\,. \]

Supposons ensuite que l'on considère une particule se déplaçant sur les points de \(\chi\). On supposera que l'évolution de cette particule est aléatoire, dans le sens où si elle se trouve à un instant donné au point \(j\in\chi\), alors à l'instant suivant (par exemple une seconde plus tard) elle se trouve au point \(i\in \chi\) avec une probabilité \(p_{ij}\). Donc pour toute paire \((i,j)\), \(p_{ij}\) représente la probabilité d'aller de \(j\)à \(i\) (appelée aussi probabilité de transition):

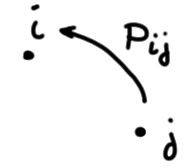
Par définition,

\(p_{ij}\in[0,1]\) pour tout \(i,j\in \chi\), et
si la particule est en \(j\) à un instant donné, elle doit bien aller quelque part à l'instant suivant, et donc \[\sum_{i\in \chi}p_{ij}=1\,.\]

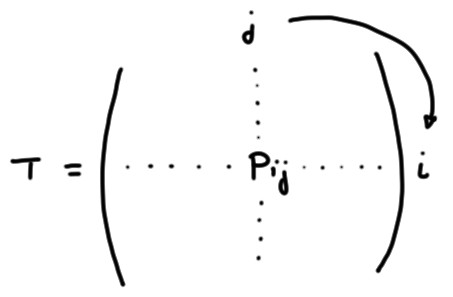
On peut stocker ces probabilités de transition dans une matrice:

Soit \(T=(p_{ij})\) une matrice \(N\times N\). On dit que \(T\) est une matrice stochastique si elle satisfait aux deux conditions ci-dessus, à savoir si

\(p_{ij}\in[0,1]\) pour tout \(i,j\in \chi\), et
la somme des éléments de chaque colonne vaut \(1\): pour tout \(j=1,2,\dots,N\), \[\sum_{i=1}^Np_{ij}=1\,.\]

On interprétera toujours les coefficients d'une matrice stochastique comme des probabilités de transition,

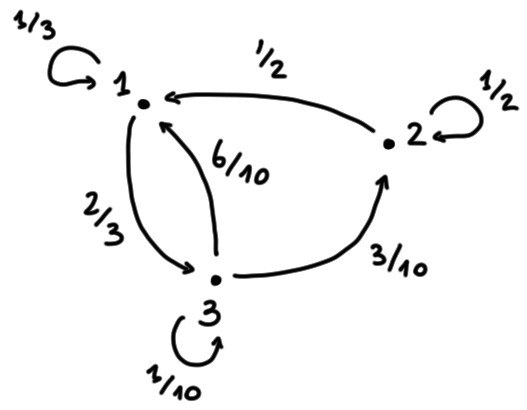
Exemple: Considérons \(\chi=\{1,2,3\}\), avec les probabilités de transition suivantes:

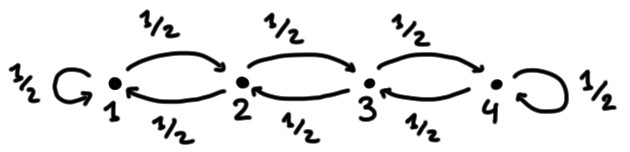
La matrice correspondante est \[ T= \begin{pmatrix} 1/3&1/2&6/10\\ 0&1/2&3/10\\ 2/3&0&1/10 \end{pmatrix} \,. \] La somme des coefficients de chaque colonne est bien toujours égale à \(1\).

Exemple: Considérons une marche aléatoire symétrique sur \(\chi=\{1,2,3,4\}\), définie par les probabilités de transition suivantes:

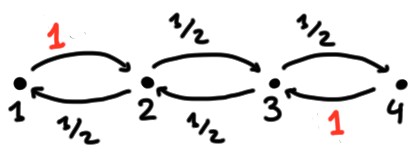
La matrice correspondante est \[ T= \begin{pmatrix} 1/2&1/2&0&0\\ 1/2&0&1/2&0\\ 0&1/2&0&1/2\\ 0&0&1/2&1/2 \end{pmatrix} \]

Exemple: Considérons une marche aléatoire sur \(\chi=\{1,2,3,4\}\), avec des barrières réfléchissantes en \(1\) et en \(4\), définie par les probabilités de transition suivantes:

La matrice correspondante est \[ T= \begin{pmatrix} 0&1/2&0&0\\ 1&0&1/2&0\\ 0&1/2&0&1\\ 0&0&1/2&0 \end{pmatrix} \]

Exemple: Considérons la marche aléatoire symétrique paresseuse sur \(\chi=\{1,2,3,4\}\), pour laquelle la probabilité de rester sur place est positive et vaut \(\varepsilon\in ]0,1[\): \[ T= \begin{pmatrix} \varepsilon&(1-\varepsilon)/2&0&0\\ 1-\varepsilon&\varepsilon&(1-\varepsilon)/2&0\\ 0&(1+\varepsilon)/2&\varepsilon&1-\varepsilon\\ 0&0&(1-\varepsilon)/2&\varepsilon \end{pmatrix} \]

Si \(\varepsilon\) est proche de \(0\), la marche n'est pas si paresseuse que ça, et son comportement est semblable à celui de celle qui a des barrières réfléchissantes.
Si \(\varepsilon\) est proche de \(1\), la marche est très paresseuse: elle reste longtemps en un point avant de se déplacer.

---- (Dernière modification: 2022-12-26 (16:26:52)) ----