7.4 Le cas \(n\times n\): matrices élémentaires et algorithme de Gauss-Jordan
Introduction

D'un point de vue très concret, le problème de l'inversibilité d'une matrice \(A\) (\(n\times n\)) peut se formuler de la façon suivante.

Puisqu'on cherche donc une matrice \(B\) (\(n\times n\)) telle que \[ AB=BA=I_n\,, \] si on écrit l'inconnue \(B\) en nommant ses colonnes, \[ B=[\boldsymbol{b}_1\cdots \boldsymbol{b}_n]\,,\] alors le produit devient \(AB=[A\boldsymbol{b}_1\cdots A\boldsymbol{b}_n]\), et comme la matrice identité peut aussi s'écrire \(I_n=[\boldsymbol{e}_1\cdots \boldsymbol{e}_n]\), la contrainte \(AB=I_n\) s'écrit \[ [A\boldsymbol{b}_1\cdots A\boldsymbol{b}_n]=[\boldsymbol{e}_1\cdots \boldsymbol{e}_n]\,. \] Les colonnes de \(B\) doivent donc être solutions des \(n\) systèmes suivants: \[ \left\{ \begin{array}{cc} (*)_1&:\, A\boldsymbol{b}_1=\boldsymbol{e}_1\,,\\ (*)_2&:\, A\boldsymbol{b}_2=\boldsymbol{e}_2\,,\\ \vdots&\\ (*)_n&:\, A\boldsymbol{b}_n=\boldsymbol{e}_n\,. \end{array} \right. \] Si on met en route l'algorithme de Gauss pour résoudre chacun de ces systèmes, on se rend compte que les opérations élémentaires faites pour résoudre le premier système \(A\boldsymbol{b}_1=\boldsymbol{e}_1\) pourront être réutilisées dans tous les systèmes suivants . On conclut que l'on peut en fait étudier la résolution de ces \(n\) systèmes en parallèle, en se concentrant uniquement sur les coefficients de la matrice \(A\).

Si on trouve des vecteurs \(\boldsymbol{b}_1,\dots,\boldsymbol{b}_n\) solutions, respectivement, de \((*)_1,\dots,(*)_n\), alors on aura déjà une matrice \(B=[\boldsymbol{b}_1\cdots \boldsymbol{b}_n]\) satisfaisant \(AB=I_n\).

Puisqu'on aimerait maintenir l'interprétation matricielle du résultat final, nous allons garder la trace des opérations élémentaires effectuées successivement, afin d'obtenir notre premier critère d'inversibilité.

Matrices élémentaires

Nous avons précédemment introduit des opérations élémentaires de Type I, II et III, qui agissaient sur un système \(m\times n\) ou, de façon équivalente, sur sa matrice augmentée. Il se trouve que chaque opération élémentaire, prise individuellement, peut se formuler à l'aide d'un produit matriciel.

Rappelons que \(I_n\) est la matrice identité \(n\times n\).

Une matrice \(n\times n\) est dite élémentaire si elle s'obtient en effectuant une (et une seule) opération élémentaire sur \(I_n\).

Exemple:

Maintenant, pour effectuer une transformation \(\mathcal{E}\) sur une matrice \(A\) (\(n\times p\)), on pourra simplement considérer la matrice élémentaire \(E\) (\(n\times n\)) obtenue en effectuant \(\mathcal{E}\) sur \(I_n\), puis l'utiliser pour multiplier \(A\) à gauche par \(E\): le résultat \(EA\) est alors la matrice \(A\) sur laquelle on a effectué \(\mathcal{E}\).

Exemple: Considérons une matrice \(3\times 4\) \[ A= \begin{pmatrix} {\color{red}a}&{\color{red}b}&{\color{red}c}&{\color{red}d}\\ {\color{blue}e}&{\color{blue}f}&{\color{blue}g}&{\color{blue}h}\\ i&j&k&l \end{pmatrix}\,. \] Supposons que l'on veuille effectuer sur \(A\) l'opération élémentaire \(\mathcal{E}\) donnée par ''\(L_1\leftrightarrow L_2\)''. Pour ce faire, on commence par appliquer \(\mathcal{E}\) à \(I_3\), qui donne \[ E= \begin{pmatrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{pmatrix}\,. \] Puis, on multiplie \(A\) par \(E\), à gauche: \[ EA= \begin{pmatrix} 0&1&0\\ 1&0&0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} {\color{red}a}&{\color{red}b}&{\color{red}c}&{\color{red}d}\\ {\color{blue}e}&{\color{blue}f}&{\color{blue}g}&{\color{blue}h}\\ i&j&k&l \end{pmatrix} = \begin{pmatrix} {\color{blue}e}&{\color{blue}f}&{\color{blue}g}&{\color{blue}h}\\ {\color{red}a}&{\color{red}b}&{\color{red}c}&{\color{red}d}\\ i&j&k&l \end{pmatrix}\,, \] qui est bien ce qu'on voulait.

Nous avions vu qu'une transformation élémentaire effectuée sur un système ne change pas son ensemble de solutions, puisqu'on pouvait toujours revenir au système de départ en appliquant une transformation réciproque. Une traduction de cette affirmation, dans le langage matriciel, est la suivante:

Lemme: Toute matrice élémentaire est inversible.

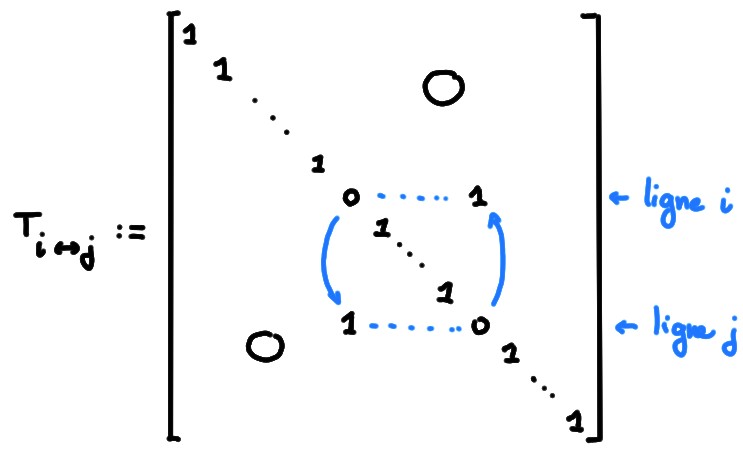
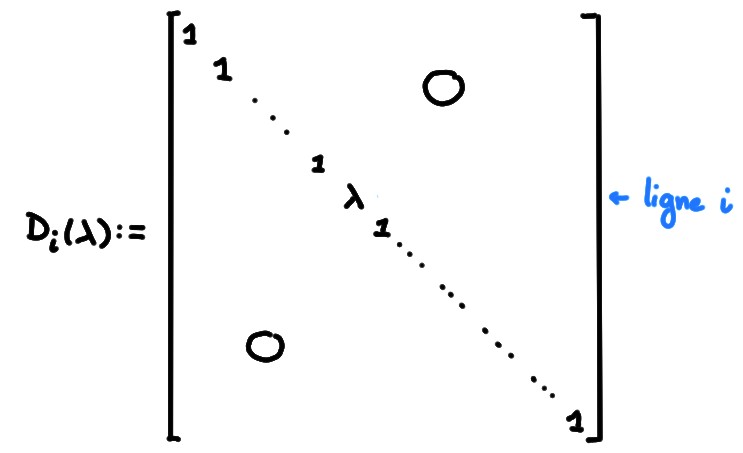
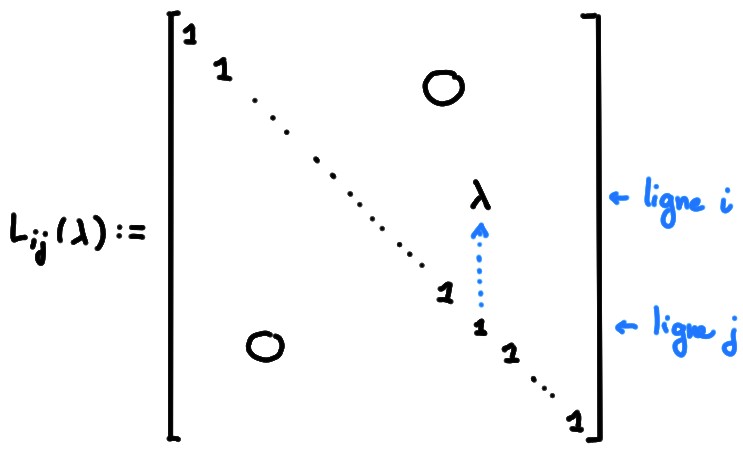
Pour le vérifier, écrivons explicitement les matrices élémentaires \(n\times n\), ainsi que leurs inverses.

Lorsqu'on résout un système, on choisit une suite d'opérations élémentaires, dans le but d'arriver à une forme échelonnée du système. Notons ces opérations \(\mathcal{E}^{(1)},\mathcal{E}^{(2)},\dots,\mathcal{E}^{(k)}\). L'application de ces opérations (d'abord \(\mathcal{E}^{(1)}\), puis \(\mathcal{E}^{(2)}\), etc.) correspondent à des multiplications successives de \(A\) à gauche par les matrices élémentaires qui leur correspondent: \[\begin{aligned} \text{Opération }\mathcal{E}^{(1)}:&\qquad E^{(1)}A\,,\\ \text{Opération }\mathcal{E}^{(1)}:&\qquad E^{(2)}E^{(1)}A\,,\\ \vdots\qquad &\\ \text{Opération }\mathcal{E}^{(k)}:&\qquad E^{(k)}\cdots E^{(2)}E^{(1)}A\,. \end{aligned}\] Comme on sait, une matrice possède une unique version échelonnée réduite, et donc il est toujours possible de bien choisir les matrices \(E^{(j)}\), de façon à ce que la matrice finale, \[\widetilde{A}=E^{(k)}\cdots E^{(2)}E^{(1)}A\,, \] soit la réduite de \(A\).

Théorème: Soit \(A\) une matrice \(n\times n\). Alors \(A\) est inversible si et seulement si on peut réduire \(A\) à l'identité \(I_n\) à l'aide d'un produit de matrices élémentaires, c'est-à-dire s'il existe des matrices élémentaires \(E^{(1)},\dots,E^{(k)}\) telles que la réduite \[ \widetilde{A}=E^{(k)}\cdots E^{(1)}A \] soit la matrice identité: \(\widetilde A=I_n\).

Supposons que \(A\) est inversible. Alors \(T(\boldsymbol{x}):= A\boldsymbol{x}\) est bijective, et par conséquent pour tout \(\boldsymbol{b}\in \mathbb{R}^n\), le système \(A\boldsymbol{x}=\boldsymbol{b}\) possède une unique solution. Ceci implique que sa forme échelonnée réduite ne présente aucune variable libre (chaque pivot est situé immédiatement à droite du pivot de la ligne supérieure). Comme \(A\) est \(n\times n\), ceci implique que la réduite de \(A\) est \(I_n\).

Supposons ensuite qu'il existe des matrices élémentaires \(E^{(1)},\dots,E^{(k)}\) telles que \[ E^{(k)}E^{(k-1)}\cdots E^{(1)}A=I_n\,. \] Rappelons que chaque \(E^{(j)}\) est inversible. En multipliant la relation ci-dessus à gauche par \((E^{(k)})^{-1}\), \[ \underbrace{(E^{(k)})^{-1}E^{(k)}}_{=I_n}E^{(k-1)} \cdots E^{(1)}A=(E^{(k)})^{-1}I_n=(E^{(k)})^{-1}\,. \] En multipliant successivement, à gauche, par \((E^{(k-1)})^{-1},\dots,(E^{(1)})^{-1}\), on arrive à \[ A=(E^{(1)})^{-1}\cdots (E^{(k)})^{-1}\,. \] Puisque chacune des matrices \((E^{(j)})^{-1}\) est inversible, \(A\) est un produit de matrices inversibles, et donc elle aussi est inversible. Son inverse est donné par \[\begin{aligned} A^{-1} &=\bigl((E^{(1)})^{-1}\cdots (E^{(k)})^{-1}\bigr)^{-1}\\ &=\bigl((E^{(k)})^{-1}\bigr)^{-1} \cdots \bigl((E^{(1)})^{-1}\bigr)^{-1}\\ &=E^{(k)}\cdots E^{(1)}\,. \end{aligned}\]

Comme conséquence de ce qui a été fait dans la preuve:

Une matrice \(A\) (\(n\times n\)) est inversible si et seulement si elle peut s'écrire comme un produit de matrices élémentaires.
L'algorithme

L'argument développé dans la preuve du précédent théorème fournit un algorithme pour déterminer si une matrice est inversible et, dans le cas où elle est inversible, de calculer son inverse.

Reprenons l'expression \[ [A\boldsymbol{b}_1\cdots A\boldsymbol{b}_n]=[\boldsymbol{e}_1\cdots \boldsymbol{e}_n]\,. \] Pour résoudre n'importe lequel de ces systèmes, \(A\boldsymbol{b}_j=\boldsymbol{e}_j\), on applique successivement des opérations élémentaires en multipliant à gauche par les matrices correspondantes \(E^{(1)},\dots,E^{(k)}\), jusqu'à obtenir, du côté gauche, la réduite de \(A\): \[\begin{aligned} A\boldsymbol{b}_j&=\boldsymbol{e}_j \\ E^{(1)}A\boldsymbol{b}_j&=E^{(1)}\boldsymbol{e}_j \\ E^{(2)}E^{(1)}A\boldsymbol{b}_j&=E^{(2)}E^{(1)}\boldsymbol{e}_j \\ \vdots&\\ \underbrace{E^{(k)}\cdots E^{(2)}E^{(1)}A}_{=\widetilde{A}}\boldsymbol{b}_j&=E^{(k)}\cdots E^{(2)}E^{(1)}\boldsymbol{e}_j \\ \end{aligned}\] Si \(\widetilde{A}=I_n\), le théorème ci-dessus dit que \(A\) est inversible; de plus la \(j\)-ème colonne de son inverse est donnée par \[ \boldsymbol{b}_j=E^{(k)}\cdots E^{(1)}\boldsymbol{e}_j\,, \] qui n'est autre que la \(j\)-ème colonne de la matrice \(E^{(k)}\cdots E^{(1)}\).

On peut résumer ce procédé dans l'algorithme suivant, appelé algorithme de Gauss-Jordan (pour l'étude de l'inversibilité d'une matrice):

  1. Commencer par considérer la matrice \(n\times 2n\) \[ \bigl(A\,\vert\,I_n\bigr)\]
  2. Considérer des opérations élémentaires permettant de transformer \(A\) en sa réduite \(\widetilde{A}\), et les appliquer simultanément sur chaque moitié: \[\begin{aligned} (A\,&\vert\, I_n)\\ (E^{(1)}A\,&\vert\,E^{(1)} I_n)\\ (E^{(2)}E^{(1)}A\,&\vert\,E^{(2)}E^{(1)} I_n)\\ \vdots&\\ (\underbrace{E^{(k)}\cdots E^{(2)}E^{(1)}A}_{=\widetilde{A}}\,&\vert\, \underbrace{E^{(k)}\cdots E^{(2)}E^{(1)}}_{=:C})\,. \end{aligned}\]
  3. Regarder le résultat obtenu, \((\widetilde{A}\,\vert\, C)\), et conclure:

Exemple: Considérons \(A= \begin{pmatrix} 1&2\\ 2&4 \end{pmatrix} \), et étudions son inversibilité à l'aide de l'algorithme ci-dessus. On pose donc \[ (A\,\vert\,I_2)= \left( \begin{array}{cc|cc} 1&2&1&0\\ 2&4&0&1 \end{array} \right) \] Comme il suffit d'une seule transformation pour réduire \(A\), \(\mathcal{E}^{(1)}=(L_2\rightarrow L_2-2L_1)\), on a \[ (\widetilde{A}\,\vert\,C)= \left( \begin{array}{cc|cc} 1&2&1&0\\ 0&0&-2&1 \end{array} \right) \] Comme \(\widetilde{A}\neq I_2\), \(A\) est singulière. (On voit aussi que \(\det(A)=0\), qui montre également que \(A\) n'est pas inversible.)

Exemple: Étudions l'inversibilité de \(A= \begin{pmatrix} 0&1&2\\ 1&0&3\\ 4&-3&8 \end{pmatrix} \). On pose \[ (A\,\vert\,I_3)= \left( \begin{array}{ccc|ccc} 0&1&2&1&0&0\\ 1&0&3&0&1&0\\ 4&-3&8&0&0&1 \end{array} \right)\,. \] Appliquons successivement des opérations élémentaires afin de réduire \(A\) du côté gauche; on applique chaque opération sur toute la matrice, y compris sur le côté droit.

Commençons par \(L_3\leftarrow L_3-4L_2\), suivie de \(L_3\leftarrow L_3+3L_1\): \[ \left( \begin{array}{ccc|ccc} 0&1&2&1&0&0\\ 1&0&3&0&1&0\\ 0&0&2&3&-4&1 \end{array} \right)\,. \] Ensuite, \(L_1\leftrightarrow L_2\), \[ \left( \begin{array}{ccc|ccc} 1&0&3&0&1&0\\ 0&1&2&1&0&0\\ 0&0&2&3&-4&1 \end{array} \right)\,, \] puis \(L_2\leftarrow L_2-L_3\), \[ \left( \begin{array}{ccc|ccc} 1&0&3&0&1&0\\ 0&1&0&-2&4&-1\\ 0&0&2&3&-4&1 \end{array} \right)\,, \] \(L_3\leftarrow \frac{1}{2}L_3\), \[ \left( \begin{array}{ccc|ccc} 1&0&3&0&1&0\\ 0&1&0&-2&4&-1\\ 0&0&1&3/2&-2&1/2 \end{array} \right)\,, \] et enfin \(L_1\leftarrow L_1-3L_3\): \[ \left( \begin{array}{ccc|ccc} 1&0&0&-9/2&7&-3/2\\ 0&1&0&-2&4&-1\\ 0&0&1&3/2&-2&1/2 \end{array} \right)\,. \] On a donc obtenu \[ (\widetilde{A}\,\vert\,C)= \left( \begin{array}{ccc|ccc} 1&0&0&-9/2&7&-3/2\\ 0&1&0&-2&4&-1\\ 0&0&1&3/2&-2&1/2 \end{array} \right)\,. \] Comme \(\widetilde{A}=I_3\), \(A\) est inversible, et son inverse est ce qu'on voit du côté droit: \[ A^{-1}= \begin{pmatrix} -9/2&7&-3/2\\ -2&4&-1\\ 3/2&-2&1/2 \end{pmatrix}\,. \] (Exercice: Pourquoi pas vérifier, à la main, que \(AA^{-1}=A^{-1}A=I_3\)!)

Dernière compilation: 2023-08-30 (14:16:45)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)