Passons à l'utilisation du produit scalaire pour introduire des
projections.
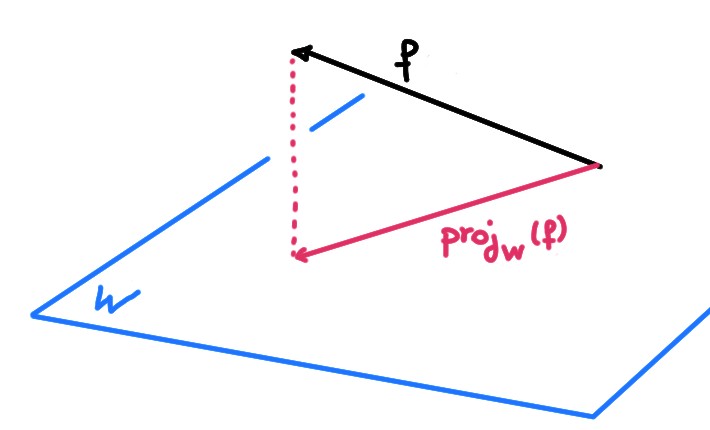
Pour commencer, la projection orthogonale
d'un \(\boldsymbol{v}\in V\) sur un \(w\in V\) est définie par
\[ \mathrm{proj}_w(v):=
\frac{(v|w)}{(w|w)}w\,.
\]
Exemple:
Si \(f,g\in C([0,\pi])\) sont définies comme dans l'exemple précédent,
\(f(t)=t\), \(g(t)=\sin(t)\), on peut calculer
\[ \mathrm{proj}_g(f)=\frac{(f|g)}{(g|g)}g
=\frac{\pi}{\frac{\pi}{2}}g=2g\,,
\]
donc \(\mathrm{proj}_g(f)\) est la fonction \(\mathrm{proj}_g(f)(t)=2\sin(t)\).
Ou encore,
\[ \mathrm{proj}_f(g)=\frac{(g|f)}{(f|f)}f
=\frac{\pi}{\frac{\pi^3}{3}}g=\frac{3}{\pi^2}f\,,
\]
donc \(\mathrm{proj}_g(f)(t)=\frac{3}{\pi^2}t\).
Nous pouvons ensuite définir la projection orthogonale d'un vecteur
\(v\in V\) sur un sous-espace \(W\subset V\) (qu'on supposera de dimension
finie) comme étant
l'unique élément \(v_\parallel\in W\) qui réalise le minimum
\[\|v-v_\parallel\|=\min_{w\in W}\|v-w\|\,.\]
On note cette projection
\[
v_\parallel= \mathrm{proj}_W(v)\,.
\]
Si \(\mathcal{B}=(w_1,\dots,w_k)\) est une base orthogonale de \(W\),
la projection s'obtient comme dans le cas de \(\mathbb{R}^n\):
\[
\mathrm{proj}_W(v)=\sum_{j=1}^k\frac{(v|w_j)}{(w_j|w_j)}w_j\,.
\]
Si la base de \(W\) n'est pas orthogonale, on pourra l'orthogonaliser à l'aide
du procédé de Gram-Schmidt.
L'intérêt d'une projection est qu'elle fournit, comme on sait,
la meilleurs approximation d'un vecteur \(v\not\in W\) par un élément de \(W\),
au sens des moindres carrés.

Exemple: Considérons, dans \(C([0,\pi])\), le sous-espace \(\mathbb{P}_2\) des polynômes de degré au plus égal à \(2\). Choisissons \(f\in C([0,\pi])\), par exemple \(f(t)=\sin(t)\), et cherchons l'élément de \(p\in \mathbb{P}_2\) qui approxime le mieux \(f\), au sens des moindres carrés. Pour ce faire, nous allons projeter \(f\) sur \(\mathbb{P}_2\), pour trouver \[ p(t)=\mathrm{proj}_{\mathbb{P}_2}(f)(t)=\lambda_0+\lambda_1t+\lambda_2t^2\,. \]
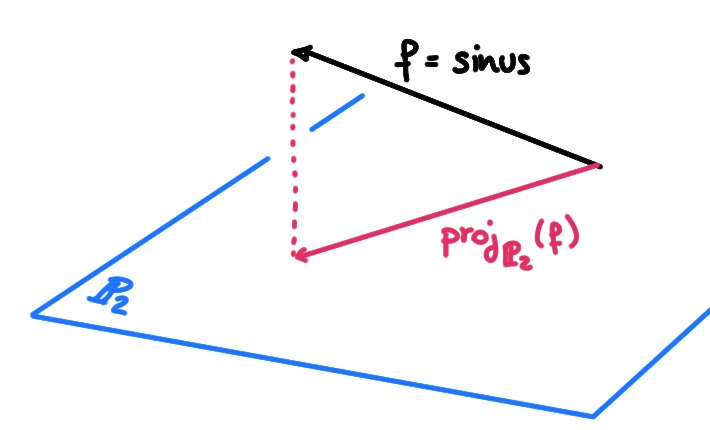
Remarque: Dans cet exemple, on a approximé la fonction \(\sin(t)\), sur \([0,\pi]\), à l'aide d'un polynôme de degré \(2\), au sens des moindres carrés: le polynôme \(p(t)\) trouvé est celui qui minimise l'intégrale \[ \int_0^\pi|\sin(t)-p(t)|^2\,dt \] Cette méthode est globale et très différente de la méthode du développement limité de l'analyse, qui est plus locale puisqu'elle a pour but de fournir une approximation précise d'une fonction au voisinage d'un point.