16.1 Définition et exemples

Les chapitres précédents ont montré à quel point l'introduction d'un produit scalaire sur \(\mathbb{R}^n\) s'est avérée utile, tant du point de vue du traitement des notions de base de l'algèbre linéaire (bases orthogonales, orthonormées, etc) que des applications (calcul de projection, approximation, moindres carrés, SVD, etc.).

Dans ce chapitre, nous allons introduire la notion de produit scalaire sur un espace vectoriel quelconque. Ceci permettra de définir la notion de perpendicularité dans un cadre très général, et d'utiliser une approche semblable à celle des derniers chapitres pour la résolution de nombreux problèmes d'approximation.

Soit \(V\) un espace vectoriel. On appelle produit scalaire une application qui à toute paire de vecteurs \(u,v\in V\) associe un réel noté \((u|v)\in\mathbb{R}\), satisfaisant aux propriétés suivantes:
  1. \((u|v)=(v|u)\) pour tous \(u,v\in V\).
  2. Pour tout \(v\in V\), l'application \(u\mapsto (u|v)\) est linéaire.
  3. Pour tout \(u\in V\), l'application \(v\mapsto (u|v)\) est linéaire.
  4. \((u|u)\geqslant 0\) pour tout \(u\in V\), et \((u|u)=0\) si et seulement si \(u=0\).
Un espace vectoriel muni d'un produit scalaire est un espace pré-Hilbertien. Un espace pré-Hilbertien de dimension finie est un espace Euclidien.

Exemple: L'espace \(\mathbb{R}^n\), muni du produit scalaire \[ (\boldsymbol{u}|\boldsymbol{v}):= \boldsymbol{u}\cdotp\boldsymbol{v} =u_1v_1+\cdots+u_nv_n\,, \] est notre premier exemple d'espace Euclidien.

Exemple: Sur l'espace vectoriel des matrices \(\mathbb{M}_{n\times n}(\mathbb{R})\), on peut vérifier que \[ (A|B):= \sum_{i=1}^m\sum_{j=1}^na_{ij}b_{ij} \] définit un produit scalaire. En effet, la symétrie et la bilinéarité sont clairement satisfaites, et \[ (A|A)= \sum_{i=1}^m\sum_{j=1}^na_{ij}^2\geqslant 0\,, \] et cette somme de carrés est nulle si et seulement chacun des carrés \(a_{ij}^2=0\), c'est-à-dire \(a_{ij}=0\), et donc \(A=0\) (la matrice nulle).

Si \(V\) est muni d'un produit scalaire \((\cdot|\cdot)\), on peut maintenant définir

Structure Euclidienne sur les espaces de fonctions

Considérons l'espace vectoriel de toutes les fonctions continues sur un intervalle fermé et borné, \(f:[a,b]\to\mathbb{R}\), noté \(C([a,b])\).

Notons (voir le cours d'Analyse 1) que les fonctions continues sont intégrables. Donc si \(f,g\in C([a,b])\), leur produit étant aussi une fonction continue, on peut définir le nombre \[ (f|g):= \int_a^bf(t)g(t)\,dt\,. \]

Lemme: Cette expression définit un produit scalaire sur \(C([a,b])\).

D'abord, \[(f|g)= \int_a^b f(t)g(t)\,dt= \int_a^b g(t)f(t)\,dt=(g|f)\,.\] Ensuite, si on fixe \(g\), alors pour tous \(f_1,f_2\in C([a,b])\), \(\lambda_1,\lambda_2\in\mathbb{R}\), les propriétés de linéarité de l'intégrale impliquent \[\begin{aligned} (\lambda_1f_1+\lambda_2f_2|g)&= \int_a^b(\lambda_1f_1(t)+\lambda_2f_2(t))g(t)\,dt\\ &= \lambda_1\int_a^b f_1(t)g(t)\,dt+ \lambda_2\int_a^b f_2(t)g(t)\,dt\\ &= \lambda_1(f_1|g)+ \lambda_2(f_2|g)\,. \end{aligned}\] En utilisant la symétrie (première propriété), et la propriété précédente, \[\begin{aligned} (f\,|\,\lambda_1g_1+\lambda_2g_2) &=(\lambda_1g_1+\lambda_2g_2\,|\,f)\\ &=\lambda_1(g_1\,|\,f)+\lambda_2(g_2\,|\,f)\\ &=\lambda_1(f\,|\,g_1)+\lambda_2(f\,|\,g_2)\,. \end{aligned}\] Puisque l'intégrale d'une fonction non-négative est non-négative, \[ (f|f)=\int_a^b\underbrace{f(t)^2}_{\geqslant 0}\,dt\geqslant 0\,. \] De plus, l'intégrale de \(f(t)^2\) est nulle si et seulement si \(f(t)=0\) pour tout \(t\in [a,b]\) (voir cours d'analyse), ce qui implique que \(f\) est la fonction identiquement nulle: \(f=0\).

Ainsi, muni de ce produit scalaire, \(C([a,b])\) est un espace pré-Hilbertien (mais pas Euclidien puisque \(C([a,b])\) est de dimension infinie). En particulier:

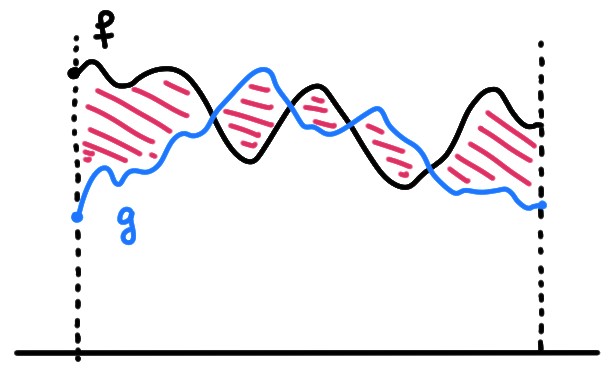
Intuitivement, deux fonctions \(f,g\) continues sur \([a,b]\) sont proches, au sens de \(\|\cdot\|\), si l'aire géométrique qui sépare leurs graphes est petite:

(Malgré tout, ce n'est pas exactement cette aire qui apparait puisqu'on intègre le carré \(|f(t)-g(t)|^2\).)

L'interprétation du produit scalaire, par contre, est moins évidente.

Exemple: Sur \(C([0,\pi])\), considérons les fonctions \(f(t):= t\) et \(g(t):= \sin(t)\), et calculons leur produit scalaire en utilisant une intégration par parties: \[\begin{aligned} (f|g) &=\int_0^\pi t\sin(t)\,dt\\ &=t(-\cos(t))\Big|_0^\pi+\int_0^\pi\cos(t)\,dt=\pi\,. \end{aligned}\] Ensuite, si \(h(t)=\cos(t)\), alors \[\begin{aligned} (g|h)&=\int_0^\pi\sin(t)\cos(t)\,dt\\ &=\frac12\int_0^\pi\sin(2t)\,dt\\ &=\frac14(-\cos(2t))\Big|_0^\pi=0\,, \end{aligned}\] donc \(g\perp h\).

Dernière compilation: 2023-08-30 (14:16:46)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)