6.2 Déterminant des matrices de taille \(2\times 2\) revisité
Propriétés algébriques du déterminant des matrices de taille \(2 \times 2\)
Nous avons déjà rencontré le déterminant lorsque nous avons étudié
l'inversibilité pour les matrices \(2\times 2\). En effet, nous avons vu qu'une
matrice
\[A=
\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}
\]
est inversible si et seulement si son déterminant, qui est le nombre
défini par
\[
\det(A):= ad-bc\,,
\]
est non-nul.
Pouvoir savoir si une matrice de taille \(2\times 2\) est
inversible ou pas, simplement en calculant un
nombre et en vérifiant s'il est nul ou pas, représente certainement
un résultat intéressant
du point de vue théorique, mais l'étendre au cas \(n\times n\) ne sera pas sans
difficulté.
En effet, dans le cas \(n\times n\),
nous avons vu quelques caractérisations équivalentes
de l'inversibilité, mais toutes étaient de nature plus calculatoire, et
toutes impliquaient plus ou moins l'étude d'un système linéaire.
Pour motiver ce que nous allons faire dans le cas de matrices de taille \(n\times n\), nous allons
revenir sur le cas de matrices de taille \(2\times 2\), et regarder de plus près cette fonction
\(A\mapsto \det(A)\), pour nous rendre compte de certaines caractéristiques,
et sans du tout nous préoccuper de l'inversibilité.
Pour le reste de cette section et le début de la section suivante, \gras{nous utiliserons plutôt
la notation ''\(\det_2\)'' au lieu de simplement \( \det \)} pour remarquer le fait que l'on travaille avec des matrices de taille \( 2 \times 2\).
En plus, plutôt que de voir une matrice de taille \(2\times 2\) comme un tableau de \(4\) nombres
rangés dans une grille, voyons la comme la donnée de deux colonnes:
\[
A= \begin{pmatrix} a&b\\ c&d \end{pmatrix}=[\boldsymbol{a}_1\,\boldsymbol{a}_2]\,,
\]
où
\[
\boldsymbol{a}_1= \begin{pmatrix} a\\ c \end{pmatrix}\,,
\boldsymbol{a}_2= \begin{pmatrix} b\\ d \end{pmatrix}\,.
\]
Ainsi, le déterminant peut être vu comme
une fonction sur les paires de vecteurs de
\(\mathbb{R}^2\), définie ainsi:
\[ {\det}_2\left(
\begin{pmatrix} a\\ c \end{pmatrix},
\begin{pmatrix} b\\ d \end{pmatrix}
\right)
:= ad-bc\,,
\]
et considérerons l'application
\[\begin{aligned}
{\det}_2:\mathbb{R}^2\times\mathbb{R}^2&\to\mathbb{R}\\
(\boldsymbol{a},\boldsymbol{b})&\mapsto \varphi(\boldsymbol{a} , \boldsymbol{b}):= a_1b_2-a_2b_1\,.
\end{aligned}\]
Les propriétés suivantes découlent entièrement de sa définition:
L'application \(\det_2\) définie ci-dessus jouit des propriétés suivantes:
- (ANT)
\(\det_2\) est antisymétrique: \(\det_2(\boldsymbol{a},\boldsymbol{b})=-\det_2(\boldsymbol{b},\boldsymbol{a})\) pour tous \(\boldsymbol{a},\boldsymbol{b} \in \mathbb{R}^2\);
- (ALT)
\(\det_2\) est alternée: \(\det_2(\boldsymbol{a},\boldsymbol{a})=0\)
pour tout \(\boldsymbol{a} \in \mathbb{R}^2\);
- (BIL)
\(\det_2\) est bilinéaire:
- (BIL.1)
pour tout \(\boldsymbol{b}\in \mathbb{R}^2\) fixé, l'application \(\boldsymbol{a}\mapsto
\det_2(\boldsymbol{a},\boldsymbol{b})\) est linéaire, i.e.
\[
{\det}_2(\boldsymbol{a}+\lambda\boldsymbol{a}',\boldsymbol{b})={\det}_2(\boldsymbol{a},\boldsymbol{b}) + \lambda {\det}_2(\boldsymbol{a}',\boldsymbol{b})
\]
pour
tout \(\lambda\in\mathbb{R}\) et \(\boldsymbol{a}, \boldsymbol{a}' \in\mathbb{R}^2\);
- (BIL.2)
pour tout \(\boldsymbol{a}\in \mathbb{R}^2\) fixé, l'application \(\boldsymbol{b}\mapsto
\det_2(\boldsymbol{a},\boldsymbol{b})\) est linéaire, i.e.
\[
{\det}_2(\boldsymbol{a},\boldsymbol{b}+\lambda\boldsymbol{b}')={\det}_2(\boldsymbol{a},\boldsymbol{b})+ \lambda{\det}_2(\boldsymbol{a},\boldsymbol{b}')
\]
pour
tout \(\lambda\in\mathbb{R}\) et \(\boldsymbol{b}, \boldsymbol{b}' \in\mathbb{R}^2\);
- (NOR) \(\det_2\) est normalisée:
\(\det_2(\boldsymbol{e}_1,\boldsymbol{e}_2) =1\).
Remarque:
On note que, si \( \varphi : \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R}\) est une application bilinéaire, alors
(ANT) et
(ALT)
pour \( \varphi \) sont équivalentes.
En effet, si
(ANT) est vraie,
alors \(\varphi(\boldsymbol{a},\boldsymbol{a})=-\varphi(\boldsymbol{a},\boldsymbol{a})\), et donc
\(\varphi(\boldsymbol{a},\boldsymbol{a})=0\).
Réciproquement, si
(ALT) est vraie, alors
\(\varphi(\boldsymbol{a}+\boldsymbol{b},\boldsymbol{a}+\boldsymbol{b})=0\), mais la bilinéarité
implique
\[\varphi(\boldsymbol{a}+\boldsymbol{b},\boldsymbol{a}+\boldsymbol{b})
=
\underbrace{\varphi(\boldsymbol{a},\boldsymbol{a})}_{=0}+
\varphi(\boldsymbol{a},\boldsymbol{b})+
\varphi(\boldsymbol{b},\boldsymbol{a})+
\underbrace{\varphi(\boldsymbol{b},\boldsymbol{b})}_{=0}\,,
\]
ce
qui nous dit que \(\varphi(\boldsymbol{b},\boldsymbol{a})=-\varphi(\boldsymbol{a},\boldsymbol{b})\).
Il se trouve que les propriétés
(BIL),
(ALT) et
(NOR) énoncées dans la proposition
caractérisent entièrement la fonction \(\det_2\):
Lemme:
Soit \(\varphi:\mathbb{R}^2\times \mathbb{R}^2\to\mathbb{R}\) une application qui
satisfait aux trois propriétés
(BIL),
(ALT) et
(NOR).
Alors, \(\varphi(\boldsymbol{a},\boldsymbol{b})=\det_2(\boldsymbol{a},\boldsymbol{b})
=a_1b_2-a_2b_1\) pour tous \( \boldsymbol{a}, \boldsymbol{b} \in \mathbb{R}^2 \).
Preuve:
On écrit d'abord
\[
\boldsymbol{a} = a_1 \boldsymbol{e}_1 + a_2 \boldsymbol{e}_2 \qquad \text{ et } \qquad \boldsymbol{b} = b_1 \boldsymbol{e}_1 + b_2 \boldsymbol{e}_2.
\]
Alors,
\[\begin{aligned}
\varphi(\boldsymbol{a},\boldsymbol{b})
&=
\varphi(a_1 \boldsymbol{e}_1 + a_2 \boldsymbol{e}_2,\boldsymbol{b})
\\
&=
a_1 \varphi(\boldsymbol{e}_1,\boldsymbol{b}) + a_2 \varphi(\boldsymbol{e}_2,\boldsymbol{b})
\\
&=
a_1 \varphi(\boldsymbol{e}_1,b_1 \boldsymbol{e}_1 + b_2 \boldsymbol{e}_2)
+ a_2 \varphi(\boldsymbol{e}_2,b_1 \boldsymbol{e}_1 + b_2 \boldsymbol{e}_2)
\\
&=
a_1 b_1 \underset{=0}{\underbrace{\varphi(\boldsymbol{e}_1,\boldsymbol{e}_1)}} + a_1 b_2 \varphi(\boldsymbol{e}_1,\boldsymbol{e}_2) + a_2 b_1\varphi(\boldsymbol{e}_2, \boldsymbol{e}_1)
+ a_2 b_2 \underset{=0}{\underbrace{\varphi(\boldsymbol{e}_2, \boldsymbol{e}_2)}}
\\
&=a_1 b_2 \varphi(\boldsymbol{e}_1,\boldsymbol{e}_2)
+ a_2 b_1 \varphi(\boldsymbol{e}_2, \boldsymbol{e}_1)
\\
&= a_1 b_2 \varphi(\boldsymbol{e}_1,\boldsymbol{e}_2) - a_2 b_1 \varphi(\boldsymbol{e}_1, \boldsymbol{e}_2)
\\
&= (a_1 b_2 - a_2 b_1) \underset{=1}{\underbrace{\varphi(\boldsymbol{e}_1, \boldsymbol{e}_2)}}
\\
&=a_1 b_2 - a_2 b_1 = {\det}_2(\boldsymbol{a},\boldsymbol{b}) ,
\end{aligned}\]
où l'on a utilisé
(BIL.1) dans la deuxième égalité,
(BIL.2) dans la quatrième égalité,
(ALT) dans la cinquième égalité,
(ANT)
dans la sixième égalité (mais l'on remarque que
(ANT) est une conséquence de
(BIL) et de
(ALT)), et
(NOR) dans l'avant-dernière égalité.
Nous verrons dans la section suivante que ces caractéristiques définissent de façon unique le déterminant
en dimensions supérieures: nous introduirons une fonction sur les familles de
\(n\) vecteurs de \(\mathbb{R}^n\), en imposant quelques propriétés semblables à
celles énoncées ci-dessus, et énoncerons un résultat qui garantit
qu'il existe une seule fonction ayant ces propriétés; c'est ce que
nous appellerons le déterminant.
L'interprétation géométrique du déterminant des matrices de taille \(2\times 2\)
Dans le plan, considérons deux vecteurs \(\boldsymbol{v},\boldsymbol{w}\), et considérons
le parallélogramme qu'ils définissent:
L'aire de ce parallélogramme, notée \(\operatorname{Aire}(\boldsymbol{v},\boldsymbol{w})\), est reliée
au déterminant de la matrice de taille \(2\times 2\) dont les colonnes sont \(\boldsymbol{v}\) et
\(\boldsymbol{w}\):
Théorème:
L'aire du parallélogramme est donnée par
\[ \operatorname{Aire}(\boldsymbol{v},\boldsymbol{w})
=
\Big|
{\det}_2
\big([\boldsymbol{v} \hskip 0.6mm \boldsymbol{w}]\big)
\Big|
=|v_1w_2-v_2w_1|\,.
\]
Preuve:
On montre d'abord que si \(A = [\boldsymbol{v} \,\, \boldsymbol{w}]\) une matrice carrée de taille \(2\) et soit \(A' = [\boldsymbol{v}' \,\, \boldsymbol{w}']\) une matrice obtenue de \(A\) en effectuant des opérations élémentaires sur les colonnes de type I et III (i.e. transposer des colonnes, et ajouter à une colonne le multiple d'une autre colonne, resp.), alors
\[
\operatorname{Aire}(\boldsymbol{v},\boldsymbol{w}) =
\operatorname{Aire}(\boldsymbol{v}',\boldsymbol{w}').
\]
En effet, comme une opération élémentaire sur les colonnes de type I sur une matrice carrée \(A\) de taille \(2\) équivaut à échanger des colonnes, on voit que le parallélogramme définis par les colonnes de \(A\) coïncide avec le parallélogramme définis par les colonnes de la matrice \(A'\) obtenue en échangeant les colonnes, et donc les aires coïncident aussi.
Pour une opération élémentaire sur les colonnes de type III sur une matrice carrée \(A\), il suffit de montrer que l’aire du parallélogramme formé par les vecteurs \(\boldsymbol{v}\) et \(\boldsymbol{w}\) est la même que l’aire du parallélogramme formé
par les vecteurs \(\boldsymbol{v}\) et \(\boldsymbol{w} + \lambda \boldsymbol{v}\), où \(\lambda \in \mathbb{R}\) est un scalaire.
Pour le faire, on rappelle que l’aire d’un parallélogramme est égale au produit de la base par la hauteur.
Les parallélogrammes indiqués ci-dessous ont la même base \(\boldsymbol{v}\) et une hauteur identique \(h\), donc la même aire.
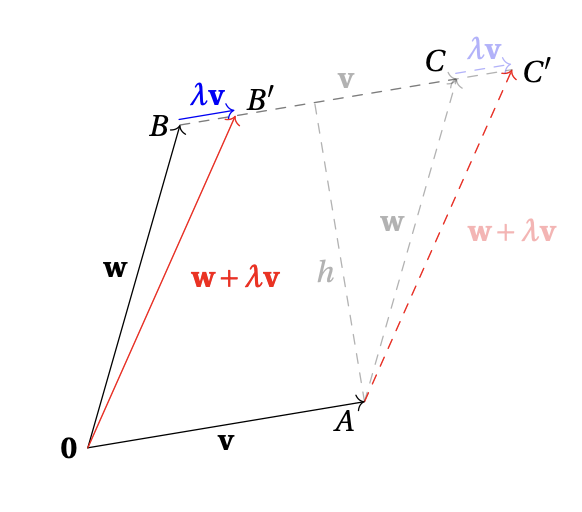
On démontre la résultat du théorème d'abord pour le cas où la matrice \(A\) n’est pas inversible,
i.e. \(\det(A) = 0\).
Dans ce cas, les colonnes de \(A\) sont obligatoirement colinéaires, et l’aire du parallélogramme formé par ces vecteurs est alors nulle.
L’assertion est donc vraie dans ce cas.
On suppose désormais que la matrice \(A\) est inversible,
i.e. \(\det(A) \neq 0\).
On écrit
\[
A = \begin{pmatrix}
a & b
\\
c & d
\end{pmatrix}.
\]
Si \(a = 0\) et \(b = 0\), alors \(a d - bc = 0\).
La contraposée nous dit alors que, comme \(\det(A) = a d - bc \neq 0\), alors \(a \neq 0\) ou \(b \neq 0\).
On s’intéresse d'abord au cas \(a \neq 0\), le cas \(b \neq 0\) se traite de la même manière en effectuant une permutation de la première et la deuxième colonnes, une opération élémentaire qui ne modifie pas la valeur absolue du déterminant ni l’aire du parallélogramme associé, d'après l'item précédent.
Or, en n'effectuant que des opérations élémentaires sur les colonnes de type III, on trouve
\[
A = \begin{pmatrix}
a & b
\\
c & d
\end{pmatrix}
\overset{C_2 \leftarrow C_2 - \frac{b}{a} C_1}{\longrightarrow}
\begin{pmatrix}
a & 0
\\
c & \frac{a d - bc}{a}
\end{pmatrix}
\overset{C_1 \leftarrow C_1 - \frac{ca}{ad - bc} C_2}{\longrightarrow}
\begin{pmatrix}
a & 0
\\
0 & \frac{a d - bc}{a}
\end{pmatrix},
\]
où \(C_i \leftarrow C_i + \lambda C_j\) désigne l'opération élémentaire qui additionne à la \(i\)-ème colonne le produit de \(\lambda \in \mathbb{R}\) par la \(j\)-ème colonne.
D'après l'item précédent, on a que
\[
\hskip -0.3cm\operatorname{Aire}\left(\begin{pmatrix}
a
\\
c
\end{pmatrix},\begin{pmatrix}
b
\\
d
\end{pmatrix}\right) =
\operatorname{Aire}\left(\begin{pmatrix}
a
\\
0
\end{pmatrix},\begin{pmatrix}
0
\\
\frac{a d - bc}{a}
\end{pmatrix}\right).
\]
Comme le dernier parallélogramme est un rectangle, on a que
\[
\operatorname{Aire}\left(\begin{pmatrix}
a
\\
0
\end{pmatrix},\begin{pmatrix}
0
\\
\frac{a d - bc}{a}
\end{pmatrix}\right)
=
|a|.\bigg|\frac{a d - bc}{a} \bigg| = |a d - bc| = \big|{\det}_2(A)\big|.
\]
En utilisant ces égalités on trouve que
\[
\operatorname{Aire}\left(\begin{pmatrix}
a
\\
c
\end{pmatrix} , \begin{pmatrix}
b
\\
d
\end{pmatrix}\right) = \big|{\det}_2(A)\big|,
\]
comme on voulait démontrer.

