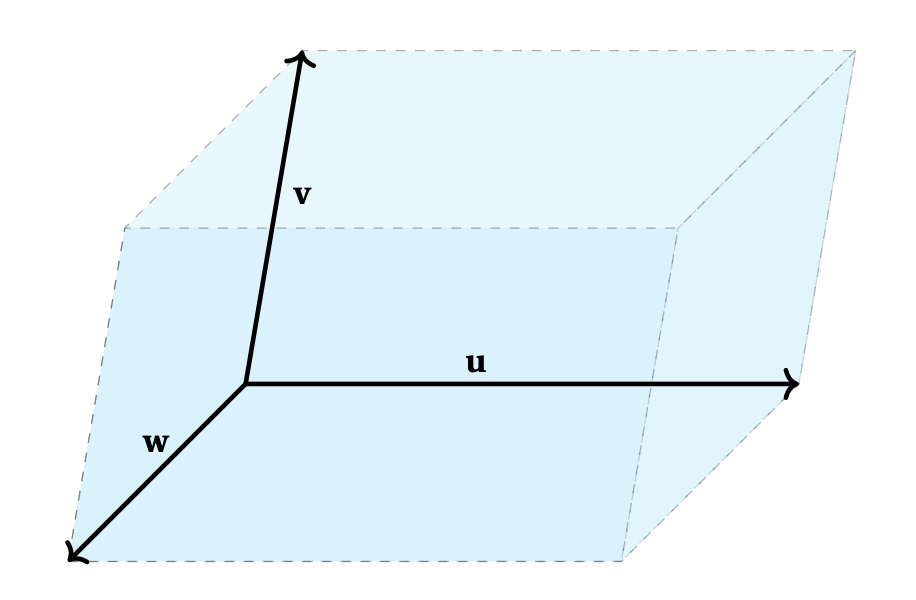
Dans l'espace, considérons trois vecteurs \(\boldsymbol{u},\boldsymbol{v},\boldsymbol{w}\), et le parallélépipède qu'ils définissent:
Le volume de ce parallélépipède, noté \(\operatorname{Vol}(\boldsymbol{u}, \boldsymbol{v},\boldsymbol{w})\), est reliée au déterminant de la matrice de taille \(3\times 3\) dont les colonnes sont \(\boldsymbol{u}\),\(\boldsymbol{v}\) et \(\boldsymbol{w}\).
Théorème: Le volume du parallélépipède est donnée par \[ \operatorname{Vol}(\boldsymbol{u},\boldsymbol{v},\boldsymbol{w}) = \Big| \det\big( [\boldsymbol{u}\hskip 0.6mm \boldsymbol{v} \hskip 0.6mm \boldsymbol{w}]\big) \Big|\,. \]
Omise.
Pour une visualisation intéressante voir la vidéo sur 3Blue1Brown .
Dernière compilation: 2025-09-02 (09:33:30)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
