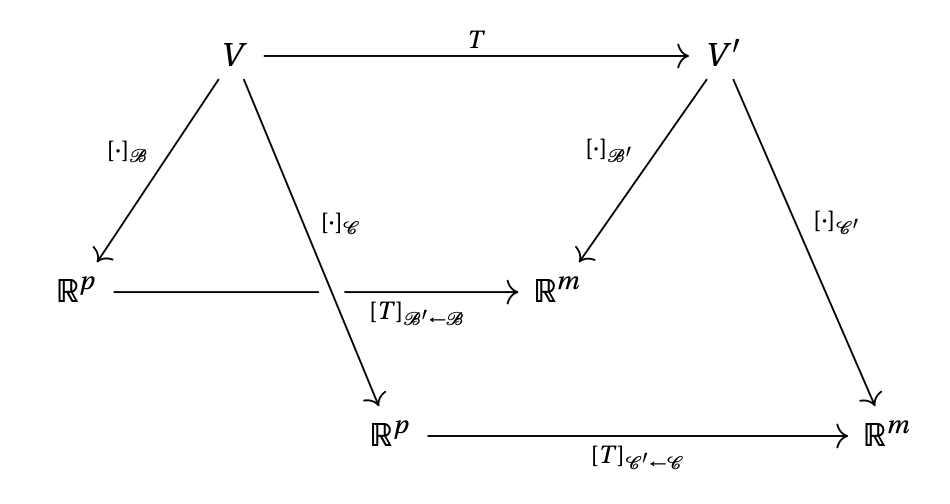
On a vu dans les sections précédentes comment exprimer une application linéaire \[T:V\to V'\,,\] lorsqu'on possède une base \(\mathcal{B}\) dans \(V\), et une base \(\mathcal{B}'\) dans \(V'\). Si l'on considère en plus une autre base \(\mathcal{C}\) de \(V\), et une base \(\mathcal{C}'\) de \(V'\), on a donc deux façons de représenter la même application linéaire \(T\), comme indiqué par la commutativité des rectangles dans le diagramme ci-dessous.
On va voir dans la sous-section suivante qu'il existe en fait une relation directe entre les deux représentations matricielles de \(T\).
Le résultat suivant est une conséquence directe mais très importante de la Proposition dans la Section (cliquer).
Théorème:[Formule de changement de base] Soient \(V\) et \(V'\) deux espaces vectoriels de dimension finie. Soient \( \mathcal{B} \) et \(calC\) deux bases de \(V\), et \( \mathcal{B}' \) et \(calC'\) deux bases de \(V'\). Pour toute application linéaire \(T:V\to V'\), on a \[ \boxed{ [T]_{\mathcal{C}'\leftarrow\mathcal{C}} =P_{\mathcal{C}'\leftarrow\mathcal{B}'} [T]_{\mathcal{B}'\leftarrow\mathcal{B}} P_{\mathcal{B}\leftarrow\mathcal{C}}\,.} \]
Comme \(T = \mathrm{id}_{V'} \circ T \circ \mathrm{id}_V \), alors le premier item de la Proposition dans la Section (cliquer) nous dit que \[ [T]_{\mathcal{C}'\leftarrow\mathcal{C}} = [\mathrm{id}_{V'} \circ T \circ \mathrm{id}_V]_{\mathcal{C}'\leftarrow\mathcal{C}} = [\mathrm{id}_{V'}]_{\mathcal{C}'\leftarrow\mathcal{B}'} [T]_{\mathcal{B}'\leftarrow\mathcal{B}} \circ [\mathrm{id}_V]_{\mathcal{C}'\leftarrow\mathcal{C}} = P_{\mathcal{C}'\leftarrow\mathcal{B}'} [T]_{\mathcal{B}'\leftarrow\mathcal{B}} P_{\mathcal{B}\leftarrow\mathcal{C}}, \] comme on voulait démontrer.
En interchangeant l'ordre des bases, le théorème précédent nous donne aussi l'identité \[ \boxed{ [T]_{\mathcal{B}'\leftarrow\mathcal{B}} =P_{\mathcal{B}'\leftarrow\mathcal{C}'} [T]_{\mathcal{C}'\leftarrow\mathcal{C}} P_{\mathcal{C}\leftarrow\mathcal{B}}\,.} \] En effet, cette formule est équivalente à celle du théorème, car on obtient la deuxième en multipliant la première à droite par \(P_{\mathcal{B}\leftarrow\mathcal{C}}\), puis à gauche par \(P_{\mathcal{C}'\leftarrow\mathcal{B}'}\).
Le théorème précédent nous permet de comprendre la relation entre les matrices \([T]_{\mathcal{B}'\leftarrow\mathcal{B}}\) et \([T]_{\mathcal{C}'\leftarrow\mathcal{C}}\), que l'on peut présenter de façon graphique avec le diagramme commutatif suivant (i.e., si l'on suit à travers le diagramme un chemin d'un objet à un autre, le résultat par composition des morphismes ne dépend que de l'objet de départ et de l'objet d'arrivée).
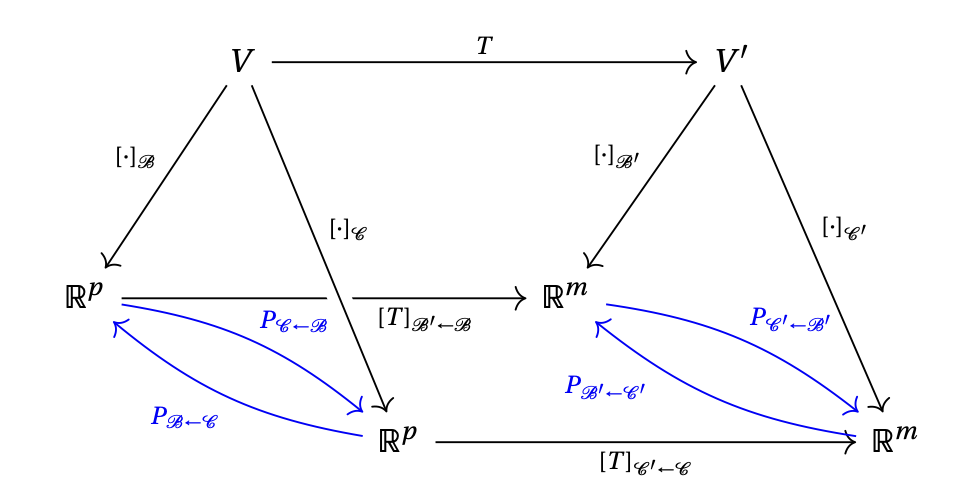
Pour simplifier un peu le schéma, gardons uniquement les espaces de départ et d'arrivée, les bases relativement auxquelles ils sont associés, ainsi que les matrices associées à \(T\) relatives à ces bases:
Le cas que nous utiliserons le plus est lorsque \(T\) applique \(V\) dans lui-même, c'est-à-dire où \(V'=V\): \[T:V\to V\,.\] Si on suppose aussi que l'on a deux bases pour décrire \(V\), \(\mathcal{B}\) et \(\mathcal{C}\), et qu'on on prend \(\mathcal{C}'=\mathcal{C}\), \(\mathcal{B}'=\mathcal{B}\), le schéma devient plus simple:
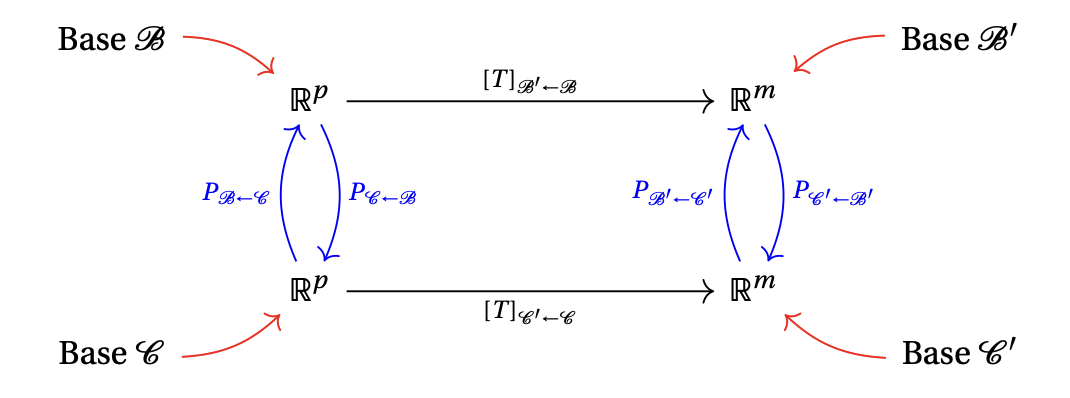
Maintenant, comme \(P_{\mathcal{B}\leftarrow\mathcal{C}}={P_{\mathcal{C}\leftarrow\mathcal{B}}}^{-1}\), la formule de changement de base du théorème précédent prend la forme plus connue: \[ \boxed{ [T]_{\mathcal{B}} ={P_{\mathcal{C}\leftarrow\mathcal{B}}}^{-1} [T]_{\mathcal{C}} P_{\mathcal{C}\leftarrow\mathcal{B}}\,,} \] ou, sinon, la version équivalente \[ \boxed{ [T]_{\mathcal{B}} = P_{\mathcal{B}\leftarrow\mathcal{C}} [T]_{\mathcal{C}} {P_{\mathcal{B}\leftarrow\mathcal{C}}}^{-1}\,.} \]
Dernière compilation: 2025-09-02 (09:33:30)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
