Dans cette section, on laisse de côté la théorie générale pour considérer
quelques
exemples importants d'applications linéaires \(T:\mathbb{R}^2\to\mathbb{R}^2\),
tous de nature géométrique.
Sur ces exemples, on
illustrera certaines des notions vues dans les sections précédentes (ensemble
image, noyau, etc.), en leur donnant un sens géométrique. On considérera aussi le
matrices associées à ces applications
relativement à la base canonique, et plus loin relativement à d'autres
bases.
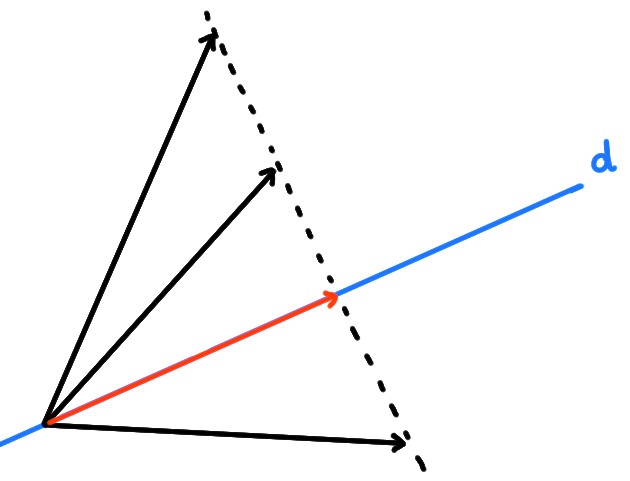
Fixons une droite \(d\) dans le plan, passant par l'origine, et considérons la transformation consistant à projeter un vecteur \(\boldsymbol{x}\in \mathbb{R}^2\) orthogonalement sur \(d\) :
Cette opération définit une application
\[\begin{aligned}
\mathrm{proj}_d:\mathbb{R}^2&\mapsto \mathbb{R}^2\\
\boldsymbol{x}&\mapsto \mathrm{proj}_d(\boldsymbol{x})\,.
\end{aligned}\]
Quelques remarques à propos de cette application:
Par définition de la projection,
tout vecteur \(\boldsymbol{v}\) appartenant à \(d\) (ou plutôt:
colinéaire à un vecteur directeur quelconque de \(d\)) ne change pas
lorsqu'il est projeté:
\[ \mathrm{proj}_d(\boldsymbol{v})=\boldsymbol{v}\,.
\]
Ceci implique en particulier que \(\mathrm{Im} (\mathrm{proj}_d)\supset d\).
Mais par définition, \(\mathrm{Im} (\mathrm{proj}_d)\subset d\), et donc
\[
\mathrm{Im} (\mathrm{proj}_d)=d\,.
\]
Puisque \(d\) est un sous-ensemble stricte de \(\mathbb{R}^2\)
, ceci implique que
\(\mathrm{proj}_d\) n'est pas surjective.
Ensuite,
\(\mathrm{proj}_d\) n'est pas injective, puisqu'il existe une infinité
de vecteurs différents dont la projection sur \(d\) est la même:

Effectivement le noyau contient (en plus du vecteur nul) une infinité de vecteurs, tous sur la droite \(d'\) perpendiculaire à \(d\), passant par l'origine:
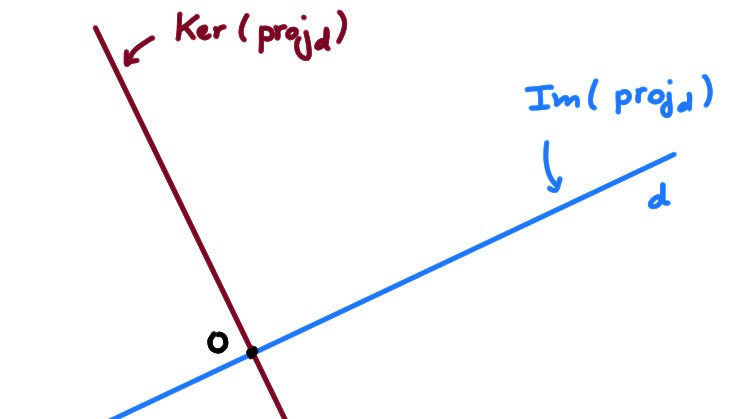
Ceci illustre aussi le théorème du rang:
\[\dim(\mathrm{Ker}(\mathrm{proj}_d))+\dim(\mathrm{Im} (\mathrm{proj}_d))=1+1=2=\dim(\mathbb{R}^2)\,.\]
Insistons sur le fait que les propriétés décrites
ci-dessus ont toutes été obtenues sans calculs.
Maintenant, la nature géométrique de la projection permet de montrer sans
peine qu'elle est linéaire.
En effet, si on multiplie \(\boldsymbol{x}\)
par un scalaire \(\lambda\), sa projection est multipliée par le même
\(\lambda\):
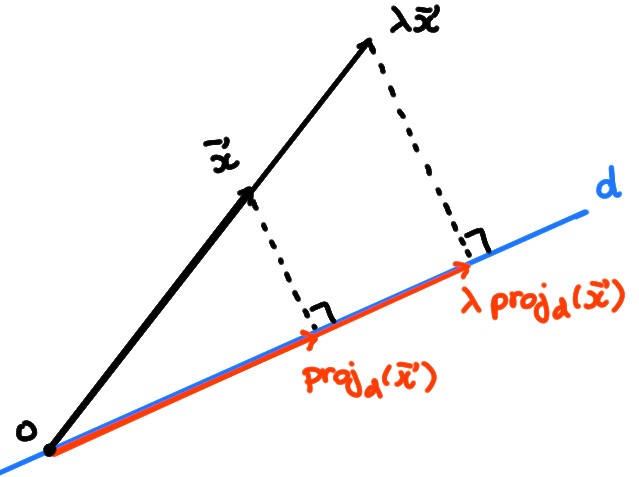
En d'autres termes: \[ \mathrm{proj}_d(\lambda \boldsymbol{x})=\lambda \mathrm{proj}_d(\boldsymbol{x})\,. \] Ensuite, si on additionne deux vecteurs et qu'ensuite on projette leur somme, on obtient le même résultat que si on les avait d'abord projetés séparément pour ensuite les additionner:
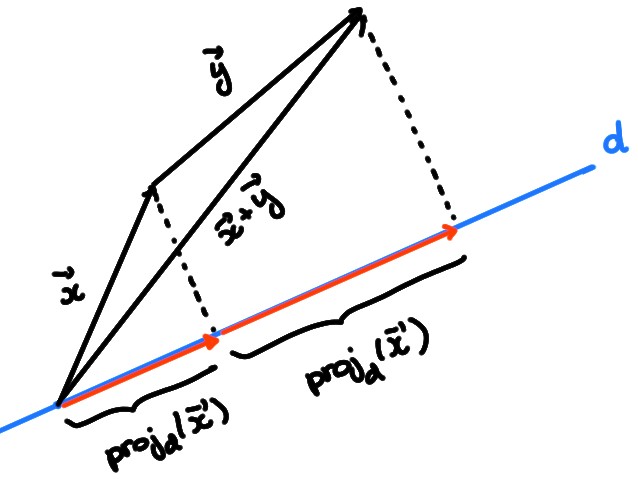
Plus précisément: \[ \mathrm{proj}_d(\boldsymbol{x}+\boldsymbol{y})=\mathrm{proj}_d(\boldsymbol{x})+\mathrm{proj}_d(\boldsymbol{y})\,. \] Maintenant, puisque \(\mathrm{proj}_d\) est linéaire, elle peut être représentée à l'aide d'une matrice. Celle-ci est donnée par \[ A=[\mathrm{proj}_d]_{\mathcal{B}_{\mathrm{can}}}=\bigl[\mathrm{proj}_d(\boldsymbol{e}_1)\,\mathrm{proj}_d(\boldsymbol{e}_2)\bigr]\,. \]
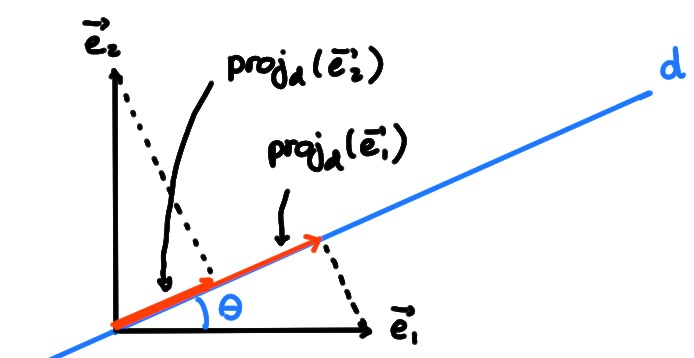
Si on suppose que \(d\) fait un angle \(\theta\) avec \(\boldsymbol{e}_1\) (dans le sens anti-horaire), on trouve \[\begin{aligned} \mathrm{proj}_d(\boldsymbol{e}_1) &=\cos(\theta) \begin{pmatrix} \cos(\theta)\\ \sin(\theta) \end{pmatrix}\\ \mathrm{proj}_d(\boldsymbol{e}_2)&= \sin(\theta) \begin{pmatrix} \cos(\theta) \\ \sin(\theta) \end{pmatrix}\,, \end{aligned}\] et donc la matrice associée à \(\mathrm{proj}_d\) est \[ [\mathrm{proj}_d]_{\mathcal{B}_{can}} = \begin{pmatrix} \cos^2(\theta)&\cos(\theta)\sin(\theta)\\ \cos(\theta)\sin(\theta)&\sin^2(\theta) \end{pmatrix} \] Comme les colonnes sont toutes deux colinéaires au vecteur directeur de \(d\), elles n'engendrent pas \(\mathbb{R}^2\), ce qui reflète le fait que \(\mathrm{proj}_d\) n'est ni injective, ni surjective.
Reprenons encore une droite \(d\) passant par l'origine, et considérons cette fois la transformation consistant à réfléchir un vecteur \(\boldsymbol{x}\in\mathbb{R}^2\) à travers \(d\). La réflexion de \(\boldsymbol{x}\) à travers \(d\) sera notée \(\mathrm{refl}_d(\boldsymbol{x})\):
Cette opération définit une application \[\begin{aligned} \mathrm{refl}_d:\mathbb{R}^2&\mapsto \mathbb{R}^2\\ \boldsymbol{x}&\mapsto \mathrm{refl}_d(\boldsymbol{x})\,. \end{aligned}\] Quelques remarques:
Comme pour la projection, on montre sans peine que \(\mathrm{refl}_d\) est une application linéaire. Calculons sa matrice relativement à la base canonique: \[ [\mathrm{refl}_d]_{\mathcal{B}_{\mathrm{can}}} =\bigl[\mathrm{refl}_d(\boldsymbol{e}_1)\,\mathrm{refl}_d(\boldsymbol{e}_2)\bigr]\,. \] Si encore une fois on suppose que \(d\) fait un angle \(\theta\) avec la direction \(\boldsymbol{e}_1\), alors on remarque que la réflexion de \(\boldsymbol{e}_1\) à travers \(d\) le transforme en un vecteur unitaire faisant un angle de \(2\theta\) avec l'horizontale:
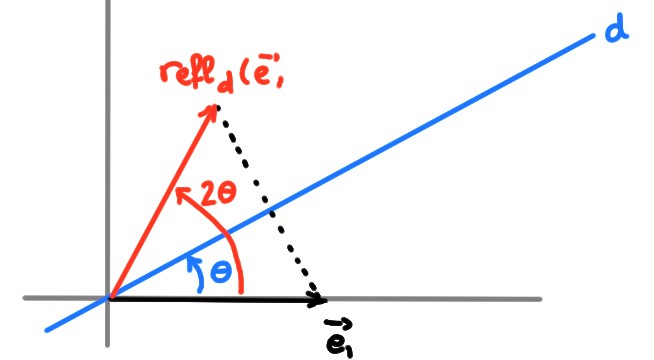
On a donc \[\mathrm{refl}_d(\boldsymbol{e}_1)= \begin{pmatrix} \cos(2\theta)\\ \sin(2\theta) \end{pmatrix}\,. \] Ensuite, la réflexion de \(\boldsymbol{e}_2\) à travers \(d\) le transforme en un vecteur unitaire faisant un angle de \(\theta-(\frac{\pi}{2}-\theta)=2\theta-\frac{\pi}{2}\) avec l'horizontale:
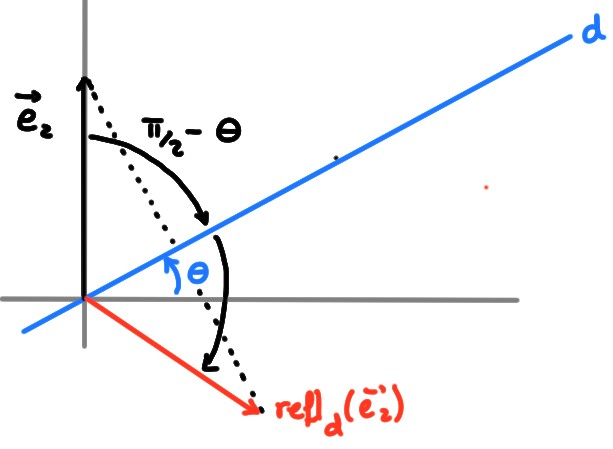
On a donc \[ \mathrm{refl}_d(\boldsymbol{e}_2)= \begin{pmatrix} \cos(2\theta-\frac{\pi}{2})\\ \sin(2\theta-\frac{\pi}{2}) \end{pmatrix}\,, = \begin{pmatrix} \sin(2\theta)\\ -\cos(2\theta) \end{pmatrix}\,. \] Ainsi, la matrice qui représente \(\mathrm{refl}_d\) relativement à la base canonique est donnée par \[ [\mathrm{refl}_d]_{\mathcal{B}_{\mathrm{can}}} = \begin{pmatrix} \cos(2\theta)&\sin(2\theta)\\ \sin(2\theta)&-\cos(2\theta) \end{pmatrix}\,. \]
Considérons une rotation d'angle \(\theta\) autour de l'origine (dans le sens trigonométrique):
Cette opération définit une application \[\begin{aligned} \mathrm{rot}_\theta:\mathbb{R}^2&\mapsto \mathbb{R}^2\\ \boldsymbol{x}&\mapsto \mathrm{rot}_\theta(\boldsymbol{x})\,. \end{aligned}\] Quelques remarques:
Une rotation (autour de l'origine) est clairement une transformation linéaire, et puisque \[ [\mathrm{rot}_\theta(\boldsymbol{e}_1)]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} \cos(\theta)\\ \sin(\theta) \end{pmatrix}\,,\qquad [\mathrm{rot}_\theta(\boldsymbol{e}_2)]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} -\sin(\theta)\\ \cos(\theta) \end{pmatrix}\,, \] sa matrice relativement à la base canonique est donnée par \[ [\mathrm{rot}_\theta]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} \cos(\theta)&-\sin(\theta)\\ \sin(\theta)&\cos(\theta) \end{pmatrix}\,. \]