5.6 Le Théorème du Rang

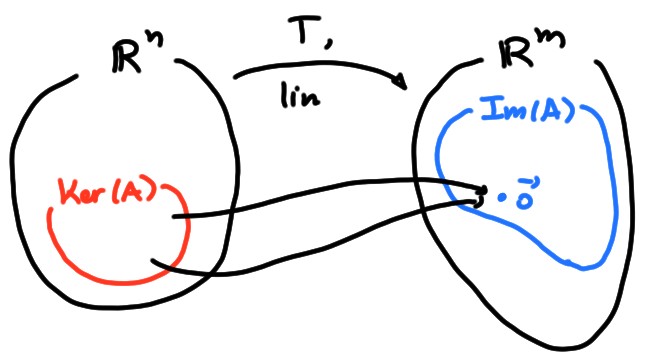
Considérons une matrice \(m\times n\), \(A\), et l'application linéaire associée, \(T(\boldsymbol{x})=A\boldsymbol{x}\):

On a déjà dit que

Dans les sections précédentes, nous avons vu comment obtenir des bases pour ces sous-espaces. Ici, nous allons compléter cette analyse en faisant quelques remarques sur les dimensions de ces espaces.

Commençons par faire une remarque sur un cas particulier:

Exemple: Considérons l'application linéaire \(T:\mathbb{R}^5\to\mathbb{R}^3\) rencontrée dans les sections précédentes, dont la matrice est \[ A= \begin{pmatrix} 1&2&0&3&-4\\ 0&-2&2&1&1\\ 1&5&-3&1&-5 \end{pmatrix}\,, \] et dont la réduite est \[ \widetilde A= \begin{pmatrix} {\color{blue}1}&0&2&0&1\\ 0&{\color{blue}1}&-1&0&-1\\ 0&0&0&{\color{blue}1}&-1 \end{pmatrix} \] Rappelons ce que nous avons déjà dit:

Par conséquent, \[\dim(\mathrm{Ker}(A))+\dim(\mathrm{Im} (A))=2+3=5\,.\] Ici, ''\(5\)'' est également la dimension de l'espace de départ (\(\mathbb{R}^5\)), qui est également égal au nombre de colonnes de \(A\).

Ce que nous venons d'observer est en fait vrai pour toute matrice: la somme des dimensions de l'ensemble image et du noyau est toujours égale à la dimension de l'espace de départ. C'est le Théorème du rang:

Théorème: Soit \(A\) une matrice \(m\times n\). Alors \[ \dim(\mathrm{Ker}(A))+\dim(\mathrm{Im} (A))=n\,. \]

Pour le même résultat, mais démontré plus généralement dans le cadre des espaces vectoriels, voir ici.

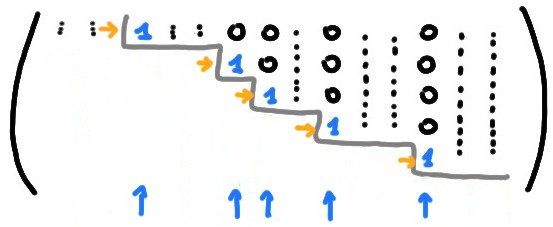
La structure générale d'une matrice réduite sera toujours du type suivant:

  • Le nombre de colonnes contenant un pivot (au nombre de \(5\) en bleu sur l'image) donne le nombre d'éléments contenus dans une base de \(\mathrm{Im} (A)\), et donc est égal à \(\dim(\mathrm{Im} (A))\).
  • Ensuite toutes les autres colonnes (au nombre de \(9\) en rouge sur l'image) représentent des variables libres, et donnent donc la dimension du noyau, \(\dim(\mathrm{Ker}(A))\). Comme il y a en tout \(n\) colonnes (\(n=14\) sur l'image), on a bien \[ \dim(\mathrm{Im} (A))+\dim(\mathrm{Ker}(A))=n\,. \]

Le terme ''rang'' doit encore être défini:

Soit \(A\) une matrice \(m\times n\). Le rang de \(A\) est défini comme la dimension de son ensemble image: \[\mathrm{rang}(A):= \dim(\mathrm{Im} (A))\,.\]

Parfois, le rang est aussi noté \(\mathrm{rg}(A)\). (En anglais: \(\mathrm{rank}(A)\).)

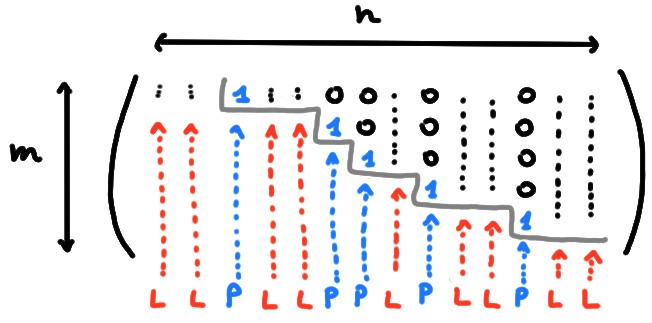
Si \(A\) est \(m\times n\), alors

  1. \(\mathrm{rang}(A)\leqslant m\). En effet, l'ensemble image de \(A\) étant un sous-espace vectoriel de \(\mathbb{R}^m\), sa dimension est au plus égale à \(m\).
  2. \(\mathrm{rang}(A)\leqslant n\). En effet, la dimension de l'ensemble image est au plus égale au nombre de colonnes de \(A\).

Par conséquent, \[ \mathrm{rang}(A)\leqslant \min\{m,n\}\,. \]

Plus le rang d'une matrice \(m\times n\) est grand, plus cette matrice définit une application qui ''remplit'' son ensemble d'arrivée. En particulier, si l'application est surjective, alors son rang vaut \(m\).

Voyons quelques exemples d'utilisation simple du théorème du rang.

Exemple: Soit \(A\) une matrice \(6\times 9\). Alors \(\mathrm{Ker}(A)\) a dimension au moins égale à \(3\). En effet, \(\mathrm{rang}(A)\leqslant \min\{6,9\}=6\), et donc par le théorème du rang, \[ \dim(\mathrm{Ker}(A))=9-\mathrm{rang}(A)\geqslant 9-6=3\,. \]

L'espace engendré par les lignes

Nous avons déjà souvent décrit un matrice \(m\times n\) à l'aide de ses colonnes \(\boldsymbol{a}_k\in \mathbb{R}^m\): \[ A=[\boldsymbol{a}_1\cdots\boldsymbol{a}_n]\,. \] Mais on peut aussi aussi la décrire à l'aide de ses lignes, \[ A= \begin{pmatrix} \boldsymbol{\ell}_1^T\\ \vdots\\ \boldsymbol{\ell}_m^T \end{pmatrix}\,, \] où \(\boldsymbol{\ell}_1,\dots,\boldsymbol{\ell}_m\) sont des vecteurs de \(\mathbb{R}^n\). En d'autres termes, les lignes de \(A\) sont les colonnes de \(A^T\): \[ A^T=[\boldsymbol{\ell}_1\cdots\boldsymbol{\ell}_m] \]

Exemple: \(\displaystyle A= \begin{pmatrix} 1&0&2\\ -4&3&5 \end{pmatrix} \) peut s'écrire \(A= \begin{pmatrix} \boldsymbol{\ell}_1^T\\ \boldsymbol{\ell}_2^T \end{pmatrix} \), où \[ \boldsymbol{\ell}_1= \begin{pmatrix} 1\\ 0\\ 2\\ \end{pmatrix}\,,\qquad \boldsymbol{\ell}_2= \begin{pmatrix} -4\\ 3\\ 5 \end{pmatrix}\,. \]

Soit \(A\) une matrice \(m\times n\), dont les lignes sont \(\boldsymbol{\ell}_1^T,\dots,\boldsymbol{\ell}_m^T\). Alors l'espace-ligne de \(A\) est le sous-espace vectoriel de \(\mathbb{R}^n\) engendré par ses lignes: \[ \mathrm{Lgn}(A):=\mathrm{Vect}\{\boldsymbol{\ell}_1,\dots,\boldsymbol{\ell}_m\}\,.\]

Lemme: Si \(A\) et \(B\) sont deux matrices équivalentes selon les lignes (on peut passer de l'une à l'autre à l'aide d'un nombre fini d'opérations élémentaires sur les lignes), alors \[ \mathrm{Lgn}(A)=\mathrm{Lgn}(B)\,. \]

Supposons que \(B\) peut s'obtenir par une suite d'opérations élémentaires sur les lignes. Alors toute combinaison linéaire des lignes de \(B\) est aussi une combinaison linéaire des lignes de \(A\). Ceci implique \(\mathrm{Lgn}(B)\subset \mathrm{Lgn}(A)\). Le même argument montre que \(\mathrm{Lgn}(A)\subset \mathrm{Lgn}(B)\), ce qui entraîne \(\mathrm{Lgn}(A)=\mathrm{Lgn}(B)\).

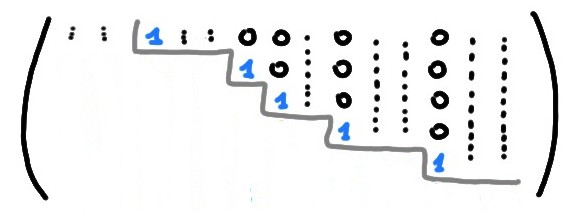
Si \(\widetilde A\) est la réduite de \(A\), alors les lignes de \(\widetilde A\) contenant un pivot (s'il y en a ) forment une base de \(\mathrm{Lgn}(\widetilde A)\) et de \(\mathrm{Lgn}(A)\).

Regardons \(\widetilde A\):

Les lignes contenant un pivot possèdent des ''\(1\)'' à des emplacements différents, précédés de ''\(0\)'': elles sont donc clairement indépendantes. Puisqu'elles engendrent évidemment \(\mathrm{Lgn}(\widetilde A)\), elles forment une base de \(\mathrm{Lgn}(\widetilde A)\).

Par le lemme précédent, toute famille de vecteurs qui forme une base de \(\mathrm{Lgn}(\widetilde A)\) forme aussi une base de \(\mathrm{Lgn}(A)\).

Intéressons-nous maintenant à la dimension de l'espace engendré par les lignes. Par définition, \[ \dim(\mathrm{Lgn}(A))=\mathrm{rang}(A^T). \] Le résultat suivant montre que les espaces engendrés par les colonnes et les lignes d'une matrice quelconque ont toujours même dimension:

Théorème: Si \(A\) est une matrice quelconque, \[ \mathrm{rang}(A)=\mathrm{rang}(A^T)\,. \]

Soit \(\widetilde A\) la réduite de \(A\). La chose importante à remarquer est que dans \(\widetilde A\), le nombre de colonnes contenant un pivot est égal au nombre de lignes non nulles. C'est évident sur un dessin:

On peut donc écrire \[\begin{aligned} \mathrm{rang}(A) &=\text{nombre de colonnes-pivot de }A\\ &=\text{nombre de colonnes contenant un pivot dans }\widetilde A\\ &=\text{nombre de lignes non-nulles dans }\widetilde A\\ &=\dim(\mathrm{Lgn}(\widetilde A))\\ &=\dim(\mathrm{Lgn}(A))\\ &=\mathrm{rang}(A^T)\,. \end{aligned}\] Dans la quatrième ligne, on a utilisé le corollaire ci-dessus. Dans la cinquième ligne, on a utilisé le lemme du dessus.

Quiz 5.6-1 : Soit \(A\) une matrice \(m\times n\), et soit \(\widetilde A\) sa réduite. Vrai ou faux?
  1. \(\mathrm{rang}(A)=\mathrm{rang}(\widetilde A)\)
  2. \(\mathrm{Im} (A)=\mathrm{Im} (A^T)\)
  3. \(\mathrm{Im} (A)=\mathrm{Im} (\widetilde A)\).

Dernière compilation: 2023-08-30 (14:16:45)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)