Dans cette section, on illustre les notions de base de la théorie des fonctions,
dans le cadre des applications linéaires \(T:\mathbb{R}^n\to\mathbb{R}^m\). En particulier,
on regardera
comment ces notions se traduisent en termes de la matrice qui représente \(T\).
Rappelons que les notions de bases de la théorie des fonctions
(injectivité, surjectivité, bijectivité) que nous utiliserons sont résumées
ici.
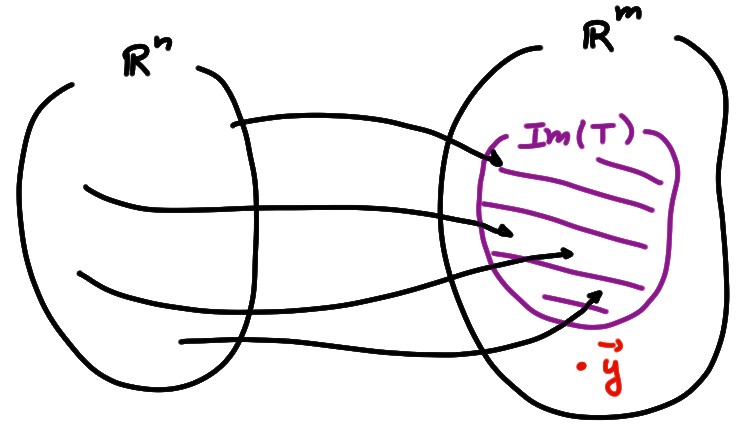
Rappelons la définition de l'ensemble image d'une application: c'est l'ensemble des points de l'ensemble d'arrivée qui possèdent au moins une préimage, \[ \mathrm{Im} (T):= \bigl\{\boldsymbol{y}\in\mathbb{R}^m\,:\,\exists \boldsymbol{x}\in\mathbb{R}^n\text{ t.q. }T(\boldsymbol{x})=\boldsymbol{y}\bigr\} \]
Rappelons aussi que
\(T:\mathbb{R}^n\to\mathbb{R}^m\) est surjective si \(\mathrm{Im} (T)=\mathbb{R}^m\).
Lorsque
\(T\) est linéaire, on sait qu'il
existe une matrice \(A\) (\(m\times n\)) telle que
\[T(\boldsymbol{x})=A\boldsymbol{x}\,.\]
Puisque \(T\) est entièrement déterminée par sa matrice \(A\), on écrira souvent
\(\mathrm{Im} (A)\) au lieu de \(\mathrm{Im} (T)\).
Écrivons maintenant \(A\) à l'aide de ses colonnes:
\[A=[\boldsymbol{a}_1\cdots \boldsymbol{a}_n]\,.\]
Puisque
\(A\boldsymbol{x}\) est une combinaison linéaire des colonnes de \(A\),
\(\mathrm{Im} (A)\) représente tous les vecteurs de \(\mathbb{R}^m\) que l'on peut obtenir
à l'aide de combinaisons linéaires des colonnes de \(A\)
:
\[\mathrm{Im} (A)=\mathrm{Vect}\{\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\}\,.\]
On peut donc se souvenir de l'ensemble image de \(T(\boldsymbol{x})=A\boldsymbol{x}\) comme
le sous-ensemble de \(\mathbb{R}^m\) engendré par les colonnes de \(A\);
pour cette raison, il est souvent noté comme suit:
\[\mathrm{Im} (T)=\mathrm{Im} (A)=\mathrm{Col}(A)\,.\]
On a donc une formulation équivalente de la surjectivité:
Théorème: Soit \(T:\mathbb{R}^n\to\mathbb{R}^m\) une application linéaire et soit \(A\) la matrice \(m\times n\) qui lui est associée. Alors \(T\) est surjective si et seulement si les colonnes de \(A\) engendrent tout \(\mathbb{R}^m\).
Exemple:
Montrons que
l'application \(T:\mathbb{R}^3\to \mathbb{R}^3\) associée à la matrice
\[
A=
\begin{pmatrix}
2&0&-1\\
1&-1&0\\
3&2&1
\end{pmatrix}
\]
est surjective. Pour ce faire, on doit fixer n'importe quel \(\boldsymbol{y}\in \mathbb{R}^3\)
et montrer qu'il existe au moins un \(\boldsymbol{x}\in \mathbb{R}^3\) tel que
\(A\boldsymbol{x}=\boldsymbol{y}\).
Fixons donc
\(\boldsymbol{y}=\begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix}\)
,
et étudions le système \(A\boldsymbol{x}=\boldsymbol{y}\):
\[
\begin{pmatrix}
2&0&-1\\ 1&-1&0\\ 3&2&1
\end{pmatrix}
\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}
=
\begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix}\,.
\]
On voit facilement que \(A\) est équivalente à
\[
\begin{pmatrix} 1&-1&0\\ 0&1&-1/2\\ 0&0&7/2 \end{pmatrix}\,,
\]
ce qui implique que la solution existe toujours (et est unique), quel que soit
\(\boldsymbol{y}\). On conclut que \(T\) est surjective: \(\mathrm{Im} (T)=\mathbb{R}^3\).
On aurait aussi pu simplement montrer que les colonnes de \(A\) forme une
famille libre, ce qui implique qu'elle engendre tout \(\mathbb{R}^3\) (c'est parce que
dans un espace vectoriel de dimension \(n\), toute famille libre de de \(n\)
vecteurs forme une base).
Exemple: L'application \(T:\mathbb{R}^2\to \mathbb{R}^4\) associée à une matrice \[ A= \begin{pmatrix} a&\alpha\\ b&\beta\\ c&\gamma\\ d&\delta \end{pmatrix} \] ne peut pas être surjective, puisque deux vecteurs de \(\mathbb{R}^4\) ne suffisent jamais pour engendrer \(\mathbb{R}^4\).
Rappelons qu'une application \(T:\mathbb{R}^n\to\mathbb{R}^m\) est injective si des éléments de \(\mathbb{R}^n\) distincts ont des images distinctes: \[\boldsymbol{x},\boldsymbol{x}'\in \mathbb{R}^n,\boldsymbol{x}\neq \boldsymbol{x}' \Rightarrow T(\boldsymbol{x})\neq T(\boldsymbol{x}')\,,\] ou alors, ce qui est équivalent, si \[ T(\boldsymbol{x})=T(\boldsymbol{x}')\quad \Longrightarrow\quad \boldsymbol{x}=\boldsymbol{x}'\,. \] Pour les applications qui sont linéaires, \(T(\boldsymbol{x})=A\boldsymbol{x}\), on sait que l'injectivité peut se caractériser à l'aide du noyau: \[ \mathrm{Ker}(T):= \bigl\{\boldsymbol{x}\in \mathbb{R}^n\,:\,A\boldsymbol{x}=\boldsymbol{0}\bigr\}\,. \]
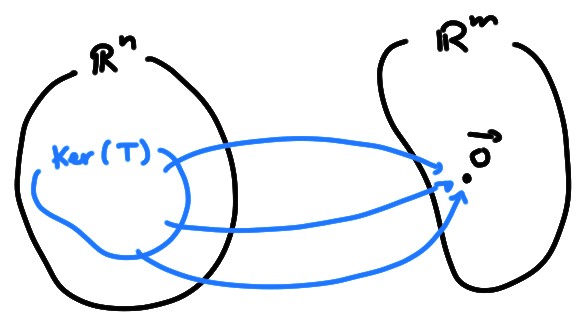
On écrira souvent le
noyau \(\mathrm{Ker}(A)\) au lieu de \(\mathrm{Ker}(T)\).
Puisque \(\mathrm{Ker}(A)\)
n'est autre que l'ensemble des
solutions du système homogène \(A\boldsymbol{x}=\boldsymbol{0}\),
et comme on sait qu'il y a toujours la solution triviale, le noyau
n'est jamais vide: \(\mathrm{Ker}(A)\ni \boldsymbol{0}\).
Nous avons vu qu'une application
linéaire est injective si et seulement si
son noyau ne contient que le vecteur nul:
\[\mathrm{Ker}(A)=\{\boldsymbol{0}\}\,.\]
Et comme on sait que l'unicité de la solution du problème homogène
caractérise l'indépendance des colonnes de \(A\),
l'injectivité peut se formuler en termes de l'indépendance des colonnes de
la matrice:
Théorème: Soit \(T:\mathbb{R}^n\to\mathbb{R}^m\) une application linéaire et soit \(A\) la matrice \(m\times n\) qui lui est associée. Alors \(T\) est injective si et seulement si les colonnes de \(A\) sont linéairement indépendantes.
Exemple: Soit \(T:\mathbb{R}^3\to\mathbb{R}^3\) l'application linéaire décrite par la matrice (déjà rencontrée plus tôt) \[ A= \begin{pmatrix} 1&1&0\\ 2&8&-2\\ 2&5&-1 \end{pmatrix} \] Puisque le noyau correspond à l'ensemble des solutions de \(A\boldsymbol{x}=\boldsymbol{0}\), on l'a déjà calculé: \[ \mathrm{Ker}(T)=\left\{ \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} =t \begin{pmatrix} -1\\ 1\\ 3 \end{pmatrix} \Big|t\in \mathbb{R} \right\} \] Comme ce noyau contient des vecteurs non-nuls (tout choix de \(t\neq 0\) donne une solution non-triviale), \(T\) n'est pas injective. Ceci signifie aussi que les colonnes de \(A\) sont linéairement dépendantes. En effet, en prenant par exemple la solution correspondant à \(t=1\), on peut écrire \[ (-1) \begin{pmatrix}1 \\2 \\2\end{pmatrix} +1 \begin{pmatrix}1 \\8 \\5 \end{pmatrix} +3 \begin{pmatrix}0 \\-2 \\-1 \end{pmatrix} = \begin{pmatrix}0 \\0 \\0 \end{pmatrix}\,. \]
Rappelons qu'une application \(T:\mathbb{R}^n\to\mathbb{R}^m\) est bijective
(ou que c'est une bijection)
si elle est à la fois surjective et injective.
La réciproque d'une application bijective \(:\mathbb{R}^n\to\mathbb{R}^m\) se note
\[\begin{aligned}
T^{-1}:\mathbb{R}^m&\to\mathbb{R}^n\\
\boldsymbol{y}&\mapsto T^{-1}(\boldsymbol{y})=\boldsymbol{x}_*\,.
\end{aligned}\]
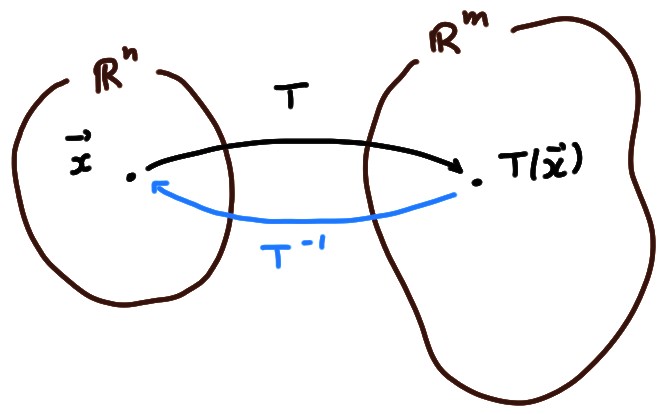
Par construction, on a \[\begin{aligned} T(T^{-1}(\boldsymbol{y}))&=\boldsymbol{y}\qquad \forall \boldsymbol{y}\in \mathbb{R}^m\,,\\ T^{-1}(T(\boldsymbol{x}))&=\boldsymbol{x}\qquad \forall \boldsymbol{x}\in \mathbb{R}^n\,. \end{aligned}\] On sait que si une application \(T:\mathbb{R}^n\to\mathbb{R}^m\) est bijective et linéaire, alors sa réciproque est aussi linéaire. Mais on a aussi:
Théorème: Si \(T:\mathbb{R}^n\to\mathbb{R}^m\) est linéaire et bijective, alors les ensembles de départ et d'arrivée doivent être de même dimension: \(m=n\).
On utilise la représentation de \(T\) à l'aide de sa matrice
\(A=[\boldsymbol{a}_1\cdots \boldsymbol{a}_n]\), où chaque \(\boldsymbol{a}_k\) est un vecteur de
\(\mathbb{R}^m\): \(T(\boldsymbol{x})=A\boldsymbol{x}\).
D'une part, \(T\) étant
injective, on sait que les colonnes de \(A\) sont linéairement
indépendantes. Ceci implique que \(n\leqslant m\) (en effet, on sait que dans
\(\mathbb{R}^m\), une famille de plus de \(m\) vecteurs est toujours liée).
D'autre part, \(T\) étant surjective, les colonnes de \(A\) engendrent
\(\mathbb{R}^m\), ce qui signifie que \(n\geqslant m\).
De là, on conclut que \(n=m\).
Ceci implique que les applications linéaire bijectives ne peuvent exister qu'entre des espaces de même dimensions: \[\begin{aligned} T:\mathbb{R}^n\to \mathbb{R}^n \end{aligned}\] De telles applications sont donc représentées par des matrices carrées. Nous y reviendrons plus tard et étudierons leurs propriétés.
Dernière compilation: 2023-08-30 (14:16:45)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
