5.3 Une base pour \(\mathrm{Im} (A)\)

Si \(T:\mathbb{R}^n\to\mathbb{R}^m\) est une application linéaire définie par une matrice \(A\) (\(m\times n\)). On sait que l'ensemble image \(\mathrm{Im} (A)=\mathrm{Col}(A)\) est un sous-espace vectoriel de \(\mathbb{R}^m\) (si \(T\) n'est pas surjective, c'est un sous-espace strict), et dans cette section nous allons voir un moyen de trouver une base pour le décrire.

Extraire une base des colonnes

D'un point de vue calculatoire, l'ensemble image \(\mathrm{Im} (A)\) se calcule en trouvant tous les \(\boldsymbol{y}\in \mathbb{R}^m\) pour lesquels le système \[ A\boldsymbol{x}=\boldsymbol{y} \] possède au moins une solution. Ensuite, chercher une base pour \(\mathrm{Im} (A)\) présente a priori une seconde étape.

Mais comme on sait, l'ensemble image est l'ensemble de toutes les combinaisons linéaires des colonnes de \(A\): \[ \mathrm{Im} (T)=\mathrm{Im} (A)=\mathrm{Col}(A)=\mathrm{Vect}\{\boldsymbol{a}_1\cdots\boldsymbol{a}_n\}\,. \] Puisque les colonnes engendrent \(\mathrm{Im} (A)\), il y a tout lieu de penser que certaines d'entre elles peuvent être utilisées pour former une base de \(\mathrm{Im} (A)\). Voyons ça sur un exemple (un peu trop) simple.

Exemple: Considérons l'application \(T:\mathbb{R}^3\to\mathbb{R}^3\) dont la matrice est donnée par \[ A= [\boldsymbol{a}_1\,\boldsymbol{a}_2\,\boldsymbol{a}_3\,\boldsymbol{a}_4] = \begin{pmatrix} 1&0&0&0\\ 0&0&0&0\\ 0&0&1&0 \end{pmatrix} \,. \] Comme \(\boldsymbol{a}_2\) et \(\boldsymbol{a}_4\) sont identiquement nulles, elles ne participent pas à \(\mathrm{Col}(A)\): \[ \mathrm{Col}(A) =\mathrm{Vect}\{\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3,\boldsymbol{a}_4\} =\mathrm{Vect}\{\boldsymbol{a}_1,\boldsymbol{a}_3\}\,. \] De plus, \(\boldsymbol{a}_1\) et \(\boldsymbol{a}_3\) sont linéairement indépendantes, et donc elles forment une base de l'espace qu'elles engendrent. Donc \(\mathcal{B}=(\boldsymbol{a}_1,\boldsymbol{a}_3)\) forme une base de \(\mathrm{Col}(A)\).

Dans ce dernier exemple, on a pu simplement retirer des colonnes nulles, sachant qu'elles ne contribuent pas à l'espace \(\mathrm{Col}(A)\).

Nous avons déjà décrit, dans le cadre abstrait des espaces vectoriels (voir ici), le processus qui permet de retirer les vecteurs ''superflus'' dans une famille qui engendre un sous-espace \(W\), donnant un algorithme menant à une base de \(W\): on retire un à un les vecteurs qui peuvent être exprimés comme combinaisons linéaires des autres, et quand on ne peut plus en retirer, c'est qu'on est en possession d'une base. Appliquons ce résultat pour calculer l'ensemble image d'une matrice, \(W=\mathrm{Col}(A)\):

Exemple: Considérons l'application linéaire \(T:\mathbb{R}^5\to\mathbb{R}^3\) dont la matrice est \[ A= [\boldsymbol{a}_1\,\boldsymbol{a}_2\,\boldsymbol{a}_3\,\boldsymbol{a}_4,\boldsymbol{a}_5]= \begin{pmatrix} 1&2&0&3&-4\\ 0&-2&2&1&1\\ 1&5&-3&1&-5 \end{pmatrix}\,. \] A priori, \[ \mathrm{Col}(A)= \mathrm{Vect}\{\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3,\boldsymbol{a}_4,\boldsymbol{a}_5\}\,. \] Or on remarque que \(\boldsymbol{a}_2=2\boldsymbol{a}_1-\boldsymbol{a}_3\), et donc le lemme ci-dessus garantit qu'on peut retirer \(\boldsymbol{a}_2\) sans changer l'espace engendré: \[ \mathrm{Col}(A)= \mathrm{Vect}\{\boldsymbol{a}_1,\boldsymbol{a}_3,\boldsymbol{a}_4,\boldsymbol{a}_5\}\,. \] On remarque aussi que \(\boldsymbol{a}_5=-\boldsymbol{a}_1+\boldsymbol{a}_3-\boldsymbol{a}_4\), et donc \[ \mathrm{Col}(A)= \mathrm{Vect}\{\boldsymbol{a}_1,\boldsymbol{a}_3,\boldsymbol{a}_4\}\,. \] Maintenant, on peut remarquer que \(\boldsymbol{a}_1\), \(\boldsymbol{a}_3\) et \(\boldsymbol{a}_4\) sont linéairement indépendantes. Comme elles engendrent \(\mathrm{Col}(A)\), elles forment donc une base de \(\mathrm{Col}(A)\).

Remarquons en passant que puisque cette base contient trois vecteurs, \(\dim(\mathrm{Col}(A))=3\), qui est aussi la dimension de l'espace d'arrivée. Ceci a pour conséquence que l'application \(T(\boldsymbol{x}):= A\boldsymbol{x}\) est surjective.

Une méthode pour identifier les colonnes retirables

Dans le dernier exemple, on a pu trouver des colonnes qui étaient combinaisons linéaires des autres, mais n'y a-t-il pas un moyen plus méthodique de trouver facilement les colonnes ''superflues'', pour ne garder que celles qui forment une base de \(\mathrm{Col}(A)\)? La réponse est ''oui'', et pour le comprendre il faut reprendre le procédé de réduction vu au début du cours.

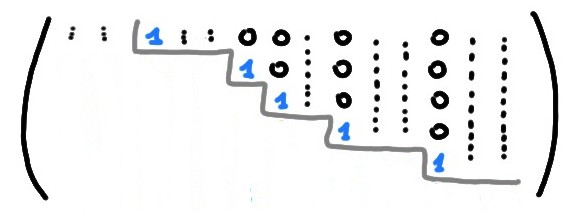
Soit \(A\) une matrice \(m\times n\) et soit \(\widetilde{A}\) sa réduite. Si la \(k\)-ème colonne de \(\widetilde A\) contient un pivot, on dit que la \(k\)-ème colonne de \(A\) est une colonne-pivot

Rappelons que les pivots, dans \(\widetilde{A}\), sont les coefficients principaux égaux à \(\color{blue}1\), seuls coefficients non-nuls de leur colonne:

L'unicité de la réduite implique que la notion de colonne-pivot, pour \(A\), est bien définie.

Exemple: Considérons \[ A= \begin{pmatrix} 3&5&-4\\ -3&-2&4\\ 6&1&-8 \end{pmatrix}\,. \] Alors les colonnes \(1\) et \(2\) de \(A\) sont des colonnes-pivot, car après réduction, les colonnes \(1\) et \(2\) de \(\widetilde A\) sont celles qui contiennent des pivots: \[ \widetilde A= \begin{pmatrix} {\color{blue} 1}&0&-4/3\\ 0&{\color{blue} 1}&0\\ 0&0&0 \end{pmatrix}\,. \]

Théorème: Les colonnes-pivot d'une matrice \(A\) forment une base de \(\mathrm{Im} (A)\). En particulier, \(\dim(\mathrm{Im} (A))\) est égale au nombre de colonnes-pivot de \(A\).

Pour démontrer le théorème, nous aurons besoin du résultat suivant, qui dit que les dépendances linéaires existant entre des colonnes d'une matrice sont les mêmes que celles existant entre les colonnes correspondantes de sa réduite:

Soit \(A=[\boldsymbol{a}_1\cdots \boldsymbol{a}_n]\), et soit \(\mathcal{F}\) un sous-ensemble de colonnes de \(A\): \[ \mathcal{F}=\{\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_l}\}\subset \{\boldsymbol{a}_1\cdots \boldsymbol{a}_n\}\,. \] Si \(\widetilde A=[\boldsymbol{r}_1\cdots \boldsymbol{r}_n]\) est la réduite de \(A\), et si \(\widetilde\mathcal{F}\) est le sous-ensemble de colonnes de \(\widetilde A\) correspondant à \(\mathcal{F}\), \[\widetilde\mathcal{F}=\{\boldsymbol{r}_{i_1},\dots,\boldsymbol{r}_{i_l}\}\subset \{\boldsymbol{r}_1\cdots \boldsymbol{r}_n\}\,, \] alors

Si les colonnes considérées sont \(i_1,\dots,i_l\), alors \[\begin{aligned} \mathcal{F}&=\{\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_l}\}\\ \widetilde\mathcal{F}&=\{\boldsymbol{r}_{i_1},\dots,\boldsymbol{r}_{i_l}\}\,. \end{aligned}\] Supposons que les colonnes de \(\mathcal{F}\) satisfont à une relation linéaire du type \[ \alpha_{i_1}\boldsymbol{a}_{i_1}+\cdots \alpha_{i_l}\boldsymbol{a}_{i_l}=\boldsymbol{0}\,. \] Cette relation représente un système homogène, et si on applique sur ce système les mêmes opérations élémentaires qui transforment \(A\) en \(\widetilde{A}\), il se transforme en le système homogène associé à la relation linéaire \[ \alpha_{i_1}\boldsymbol{r}_{i_1}+\cdots \alpha_{i_l}\boldsymbol{r}_{i_l}=\boldsymbol{0}\,. \] Puisque les opérations élémentaires ne changent pas l'ensemble des solutions d'un système, des nombres \(\alpha_{i_1},\dots,\alpha_{i_l}\) sont solutions de la première relation si et seulement ils sont solutions de la deuxième relation. Ceci démontre la proposition.

Exemple: Les colonnes \(1\), \(3\) et \(8\) de \(A\) sont dépendantes si et seulement si les colonnes \(1\), \(3\) et \(8\) de \(\widetilde A\) sont dépendantes.

Une conséquence directe du résultat ci-dessus:

Un sous-ensemble des colonnes de \(A\) \[ \mathcal{B}=(\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_l})\subset \{\boldsymbol{a}_1\cdots \boldsymbol{a}_n\} \] forme une base de \(\mathrm{Col}(A)\) si et seulement si le sous-ensemble de colonnes de \(\widetilde A\) correspondant, \[\widetilde\mathcal{B}=(\boldsymbol{r}_{i_1},\dots,\boldsymbol{r}_{i_l})\subset \{\boldsymbol{r}_1\cdots \boldsymbol{r}_n\}\,, \] forme une base de \(\mathrm{Col}(\widetilde A)\).

Exemple: Soit \(A\) une matrice \(7\times 11\). Les colonnes \(2\), \(5\) et \(8\) de \(\widetilde A\) forment une base de \(\mathrm{Col}(\widetilde A)\) si et seulement si les colonnes \(2\), \(5\) et \(8\) de \(A\) forment une base de \(\mathrm{Col}(A)\).

Nous pouvons maintenant prouver le théorème:

Commençons par deux remarques concernant la réduite \(\widetilde A\).

  • Dans \(\widetilde A\), les colonnes contenant des pivots sont linéairement indépendantes, puisqu'elles ont toutes un seul coefficient non nul (le pivot ''\(1\)''), chaque fois situé à une hauteur différente.
  • Dans \(\widetilde A\), toute colonne qui ne contient pas de pivot peut s'écrire comme combinaison linéaire des colonnes qui contiennent un pivot, et qui sont situées à sa gauche.
Par conséquent, le lemme énoncé plus haut garantit que les colonnes de \(\widetilde A\) ne contenant pas de pivot ne contribuent pas à \(\mathrm{Col}(\widetilde A)\), et les colonnes contenant un pivot forment une base de \(\mathrm{Col}(\widetilde A)\). Par le corollaire, ceci implique que les colonnes-pivot de \(A\) forment une base de \(\mathrm{Col}(A)\).

Voyons comment utiliser le théorème pour obtenir plus facilement une base de \(\mathrm{Col}(A)\):

Exemple: Considérons la même matrice que celle du début de cette section: \[ A= [\boldsymbol{a}_1\,\boldsymbol{a}_2\,\boldsymbol{a}_3\,\boldsymbol{a}_4,\boldsymbol{a}_5]= \begin{pmatrix} 1&2&0&3&-4\\ 0&-2&2&1&1\\ 1&5&-3&1&-5 \end{pmatrix}\,. \] Après réduction, \[ \widetilde A= \begin{pmatrix} {\color{blue}1}&0&2&0&1\\ 0&{\color{blue}1}&-1&0&-1\\ 0&0&0&{\color{blue}1}&-1 \end{pmatrix} \] Comme les colonnes \(1,2\) et \(4\) de \(\widetilde A\) sont celles contenant des pivots, on conclut que \(\mathcal{B}=(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_4)\) est une base de \(\mathrm{Col}(A)\) . En particulier, \(\dim(\mathrm{Im} (A))=3\).

Quiz 5.3-1 : Soit \(A\) une matrice \(m\times n\), et soit \(\widetilde{A}\) sa réduite. Vrai ou faux?
  1. Pour trouver une base de \(\mathrm{Im} (A)\) on prend les colonnes de \(\widetilde{A}\) qui contiennent un pivot.
  2. Si \(A=[\boldsymbol{a}_1\cdots \boldsymbol{a}_n]\), et si \(\widetilde{A}\) contient \(k\) pivots, alors \(\{\boldsymbol{a}_1,\dots,\boldsymbol{a}_k\}\) est une base de \(\mathrm{Im} (A)\).
  3. La dimension de \(\mathrm{Im} (A)\) est égale au nombre de colonnes de \(\widetilde{A}\) contenant un pivot.
  4. \(\mathrm{Col}(A)=\mathrm{Col}(\widetilde{A})\).

Dernière compilation: 2023-08-30 (14:16:45)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)