Analyse réelle | S. Friedli

8.3 Effet sur la matrice d'une application

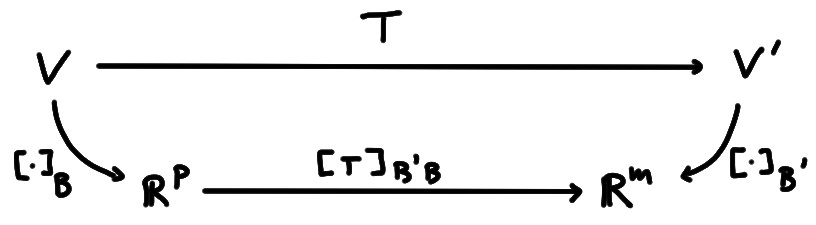
On a vu dans le chapitre sur les espaces vectoriels comment exprimer une application linéaire \[T:V\to V'\,,\] lorsqu'on possède une base \(\mathcal{B}\) dans \(V\), et une base \(\mathcal{B}'\) dans \(V'\):

\(\mathcal{B}=(v_1,\dots,v_p)\) est une base de \(V\),
\(\mathcal{B}'=(v_1',\dots,v_m')\) est une base de \(V'\).

Rappelons que si \(v\in V\), et si \(v'=T(v)\in V'\) est son image, alors la représentation matricielle de cette correspondance s'exprime par \[ \underbrace{[T(v)]_{\mathcal{B}'}}_{\in \mathbb{R}^m}= \underbrace{[T]_{\mathcal{B}'\mathcal{B}}}_{m\times p}\underbrace{[v]_{\mathcal{B}}}_{\in \mathbb{R}^p}\,, \] où les colonnes de la matrice \([T]_{\mathcal{B}'\mathcal{B}}\) s'obtiennent en décomposant les images des vecteurs de \(\mathcal{B}\) dans \(\mathcal{B}'\): \[ [T]_{\mathcal{B}'\mathcal{B}}= \bigl[ [T(v_1)]_{\mathcal{B}'}\cdots [T(v_p)]_{\mathcal{B}'} \bigr] \]

Changement de base dans le cas général \(T:V\to V'\)

Supposons maintenant que l'on ait d'autres bases qui décrivent les espaces de départ et d'arrivée, disons \(\mathcal{C}\) dans \(V\) et \(\mathcal{C}'\) dans \(V'\):

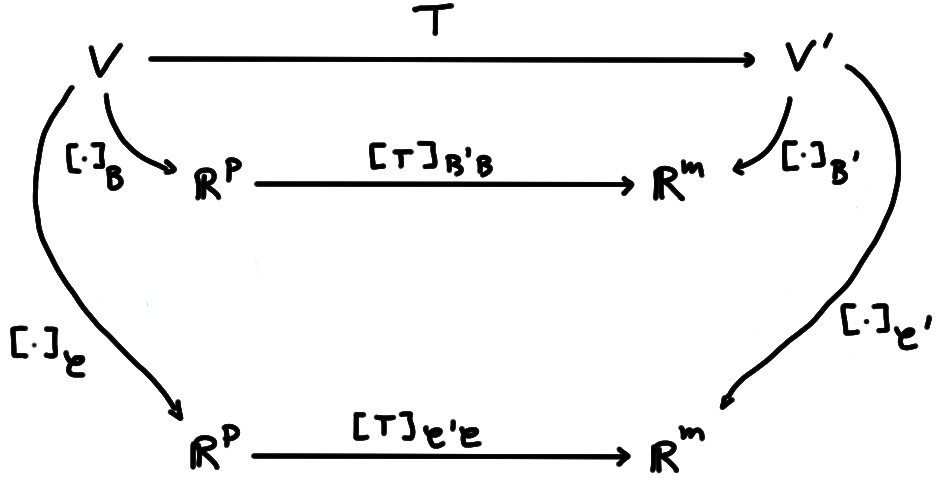
On a donc deux façons de représenter la même application linéaire \(T\):

En utilisant les bases \(\mathcal{B}\) et \(\mathcal{B}'\): \[ [v]_{\mathcal{B}}\mapsto [T(v)]_{\mathcal{B}'}=[T]_{\mathcal{B}'\mathcal{B}}[v]_{\mathcal{B}}\,.\]
En utilisant les bases \(\mathcal{C}\) et \(\mathcal{C}'\): \[ [v]_{\mathcal{C}}\mapsto [T(v)]_{\mathcal{C}'}=[T]_{\mathcal{C}'\mathcal{C}}[v]_{\mathcal{C}}\,.\]

Notre but ici est de comprendre la relation entre les matrices \([T]_{\mathcal{B}'\mathcal{B}}\) et \([T]_{\mathcal{C}'\mathcal{C}}\).

Considérons les matrices de changement de base construites dans la section précédente, \(P_{\mathcal{C}\mathcal{B}}\) et \(P_{\mathcal{C}'\mathcal{B}'}\), et leurs inverses:

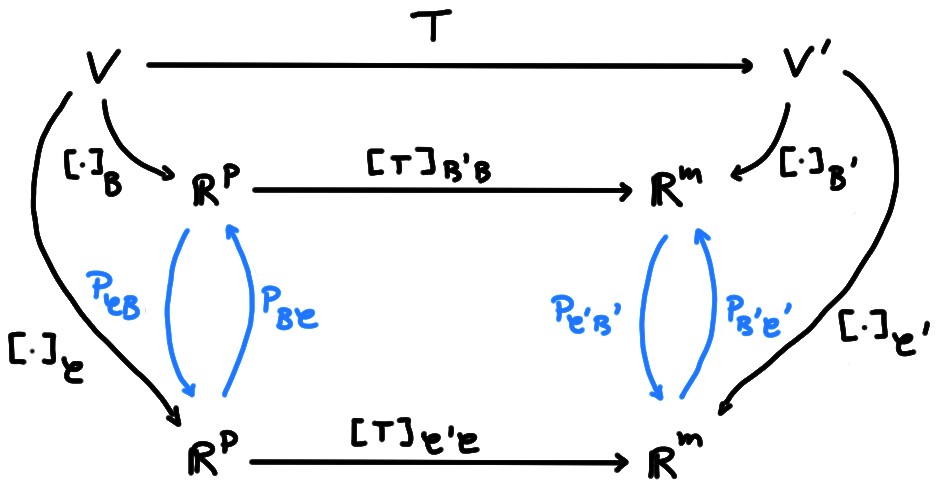
Pour simplifier un peu le schéma, gardons uniquement les espaces de départ et d'arrivée, les bases relativement auxquelles ils sont associés, ainsi que les matrices associées à \(T\) relativement à ces bases:

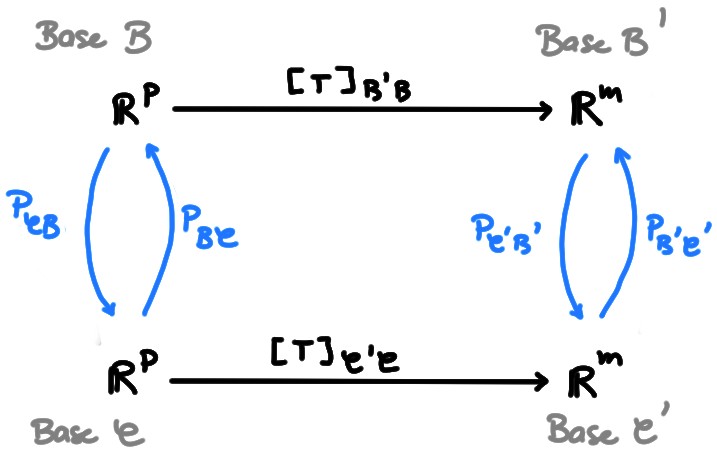
Dans ce diagramme, on peut monter ou descendre librement à l'aide des matrices de changement de base, puisqu'elles sont inversibles . On a donc les formules de changement de base: \[ \boxed{ [T]_{\mathcal{B}'\mathcal{B}} =P_{\mathcal{B}'\mathcal{C}'} [T]_{\mathcal{C}'\mathcal{C}} P_{\mathcal{C}\mathcal{B}}}\,, \] et \[ \boxed{ [T]_{\mathcal{C}'\mathcal{C}} =P_{\mathcal{C}'\mathcal{B}'} [T]_{\mathcal{B}'\mathcal{B}} P_{\mathcal{B}\mathcal{C}}}\,. \]

Ces deux formules sont équivalentes: on obtient la deuxième en multipliant la première à droite par \(P_{\mathcal{B}\mathcal{C}}\), puis à gauche par \(P_{\mathcal{C}'\mathcal{B}'}\).

Changement de base dans le cas \(T:V\to V\)

Le cas que nous utiliserons le plus est lorsque \(T\) applique \(V\) dans lui-même, c'est-à-dire où \(V'=V\): \[T:V\to V\,.\] Dans ce cas, on a \(p=m\). Si on suppose aussi que l'on a deux bases pour décrire \(V\), \(\mathcal{B}\) et \(\mathcal{C}\), et qu'on on prend \(\mathcal{C}'=\mathcal{C}\), \(\mathcal{B}'=\mathcal{B}\), le shéma devient plus simple:

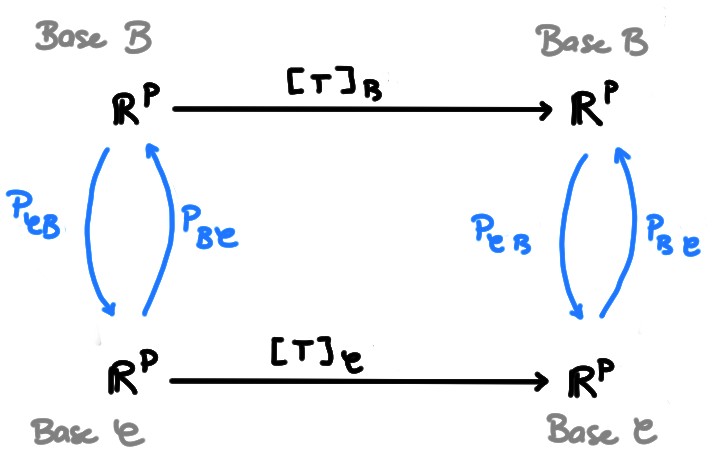
Maintenant, comme \(P_{\mathcal{B}\mathcal{C}}={P_{\mathcal{C}\mathcal{B}}}^{-1}\), les formules de changement de base prennent la forme plus connue: \[ \boxed{ [T]_{\mathcal{B}} ={P_{\mathcal{C}\mathcal{B}}}^{-1} [T]_{\mathcal{C}} P_{\mathcal{C}\mathcal{B}}\,,} \] on encore \[ \boxed{ [T]_{\mathcal{B}} = P_{\mathcal{B}\mathcal{C}} [T]_{\mathcal{C}} {P_{\mathcal{B}\mathcal{C}}}^{-1}\,.} \]