15.1 Introduction

'' Today, singular value decomposition has spread through many branches of science, in particular psychology and sociology, climate and atmospheric science, and astronomy. It is also extremely useful in machine learning and in both descriptive and predictive statistics. ''

Peter Mills

'' Eigenvalues and eigenvectors are restricted to square matrices. But data comes in rectangular matrices. ''

Gilbert Strang

Si la diagonalisation a permis de comprendre la nature géométrique de certaines applications linéaires, elle exige malheureusement que l'application considérée se prête à cette analyse (qu'elle soit diagonalisable justement), et surtout: elle ne s'applique qu'à des matrices carrées.

Le résultat

La décomposition en valeurs singulières (SVD\(=\)Singular Value Decomposition) est une méthode très générale de factorisation qui donne une nouvelle interprétation géométrique de n'importe quelle application linéaire \(T:\mathbb{R}^n\to\mathbb{R}^m\). Elle consiste à factoriser une matrice quelconque \(A\) (\(m\times n\)) en un produit, \[ A= {\color{green}U} {\color{blue}\Sigma} {\color{magenta} V^T}\,, \] où

1. \({\color{green}U}\) est \(m\times m\), orthogonale: \(U^TU=UU^T=I_m\),
2. \({\color{blue}\Sigma}\) est \(m\times n\), diagonale dans le sens où \(\Sigma_{ij}=0\) si \(i\neq j\). De plus, \(\Sigma_{ij}\geqslant 0\).
3. \({\color{magenta} V}\) est \(n\times n\), orthogonale: \(V^TV=VV^T=I_n\).

On sait d'une part que les matrices orthogonales représentent des isométries, c'est-à-dire des transformations rigides de l'espace, et doivent être comprises essentiellement comme des rotations. D'autre part, une matrice diagonale \(m\times n\) a pour effet de stretcher certaines directions (avec un changement de dimension, voir plus bas). Donc la décomposition en valeurs singulières permet de décomposer l'application \(T:\mathbb{R}^n\to\mathbb{R}^m\) définie par \(T(\boldsymbol{x})=A\boldsymbol{x}\) en trois parties: \[ \mathbb{R}^n \stackrel{{\color{magenta}\stackrel{V^T}{\text{(rotation)}}}}{\longrightarrow} \mathbb{R}^n \stackrel{{\color{blue}\stackrel{\Sigma}{\text{(stretch)}}}}{\longrightarrow} \mathbb{R}^m \stackrel{{\color{green}\stackrel{U}{\text{(rotation)}}}}{\longrightarrow} \mathbb{R}^m \] Il est important d'insister sur le fait que la décomposition en valeurs singulières ne suppose rien sur \(A\); elle est toujours possible. En particulier, elle s'applique à des matrices qui ne sont pas forcément carrées.

Structure

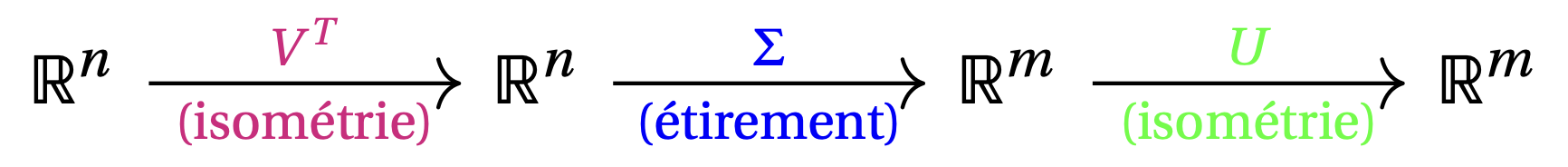
Dans la section suivante, nous établirons rigoureusement la décomposition en valeurs singulières. Pour l'instant, supposons qu'une décomposition \[ A= U \Sigma V^T \] soit donnée, et voyons ce que cela dit déjà sur les matrices \(U\), \(\Sigma\) et \(V\).

Nommons les colonnes de \(V\), \(U\) et \(\Sigma\): \[\begin{aligned} U&=[\boldsymbol{u}_1 \cdots \boldsymbol{u}_m]\qquad \boldsymbol{u}_k\in\mathbb{R}^m\\ \Sigma&=[\boldsymbol{\sigma}_1 \cdots \boldsymbol{\sigma}_n]\qquad \boldsymbol{\sigma}_i\in\mathbb{R}^m\\ V&=[\boldsymbol{v}_1 \cdots \boldsymbol{v}_n]\qquad \boldsymbol{v}_j\in\mathbb{R}^n\,. \end{aligned}\] Puisque \(U\) et \(V\) sont orthogonales, les familles \(\{\boldsymbol{u}_1,\dots,\boldsymbol{u}_m\}\subset\mathbb{R}^m\) et \(\{\boldsymbol{v}_1,\dots,\boldsymbol{v}_n\}\subset\mathbb{R}^n\) sont orthogonales.

La matrice \(\Sigma\) représente une application \(\mathbb{R}^n\to\mathbb{R}^m\) dont la simplicité rappelle celle des matrices diagonales carrées. Nous noterons \(\sigma_i\) les éléments diagonaux de \(\Sigma\). Notons que si \(m\gt n\) (resp. \(m\lt n\)), alors certaines lignes (resp. colonnes) de \(\Sigma\) sont nulles.

Pour comprendre les relations entre les \(\boldsymbol{u}_k\), les \(\boldsymbol{v}_j\) et la matrice \(\Sigma\) (toujours en supposant que la décomposition \(A=U\Sigma V^T\) est déjà connue), on multiplie \(A\) par sa transposée pour obtenir une matrice \(n\times n\) donnée par \[\begin{aligned} A^TA &=(U\Sigma V^T)^T(U\Sigma V^T)\\ &=V\Sigma^TU^TU\Sigma V^T \\ &=V(\Sigma^T\Sigma)V^T \end{aligned}\] On a, dans le terme de droite, trois matrices \(n\times n\). Puisque \(\Sigma^T\Sigma\) est diagonale, et puisque \(V^T\) est l'inverse de \(V\) (car cette dernière est orthogonale), on voit que ce produit de trois matrices carrées représente une diagonalisation de la matrice symétrique \(A^TA\). En particulier, les colonnes de \(V\) sont des vecteurs propres orthonormés de \(A^TA\), associés à des valeurs propres qui sont les éléments diagonaux de \(\Sigma^T\Sigma\), à savoir \(\sigma_i^2\): \[ (A^TA) \boldsymbol{v}_j=\sigma_j^2 \boldsymbol{v}_j \qquad \forall j=1,\dots,n\,. \] De même pour \(AA^T\): c'est une matrice \(m\times m\), et \[ AA^T=U(\Sigma\Sigma^T)U^T\,, \] qui implique que les colonnes de \(U\) sont des vecteurs propres orthonormés de \(AA^T\), associés à des valeurs propres qui sont les éléments diagonaux de \(\Sigma\Sigma^T\): \[ AA^T \boldsymbol{u}_k=\sigma_k^2 \boldsymbol{u}_k \qquad \forall k=1,\dots,m\,. \]

Remarquons encore que dans les deux cas, les matrices diagonales \(\Sigma^T\Sigma\) et \(\Sigma\Sigma^T\) ont des coefficients diagonaux donnés par les carrés \(\sigma_i^2\).

Cette discussion montre que si une décomposition en valeurs singulières existe, alors les matrices \(U\) et \(V\) se calculent en diagonalisant \(AA^T\) et \(A^TA\). (On verra comment simplifier un peu ce procédé par la suite.)

Ce qui n'est pas du tout démontré par l'argument ci-dessus, c'est si la décomposition existe effectivement; nous le démontrerons dans la section suivante.

Matrices définies par blocs

Dans ce chapitre, nous définirons et manipulerons des matrices définies par blocs, ce qui signifie définies comme composées de sous-matrices. On utilisera l'indice ''\(\square\)'' pour indiquer qu'une matrice est définie par blocs.

Les blocs qui composent une matrice par blocs doivent avoir des dimensions compatibles.

Plus généralement, si on possède quatre matrices, \[ A\,(m\times k),\quad B\,(m\times l),\quad C\,(h\times k),\quad D\,(h\times l), \] on peut définir

• la matrice \(m\times (k+l)\): \[ \left[ \begin{array}{cc} A&B \end{array} \right]_{\square}\,, \]
• la matrice \((m+h)\times k\): \[ \left[ \begin{array}{cc} A\\ C \end{array} \right]_{\square}\,. \]
• la matrice \((m+h)\times (k+l)\): \[ \left[ \begin{array}{cc} A&B\\ C&D \end{array} \right]_{\square}\,. \]

---

Dernière compilation: 2023-08-30 (14:16:46)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)