14.3 Exemples
La preuve de la section précédente a montré clairement quelles sont les étapes
menant à une décomposition singulière d'une matrice \(A\):
Méthode pour calculer la décomposition en valeurs singulières \(U \Sigma V^T\)
d'une matrice \(A \in \mathbb{M}_{m \times n(\mathbb{R})\).}
- (SVD.1) Calculer les valeurs propres \(\lambda_1 \geqslant \dots \geqslant \lambda_n \geqslant 0\) de \(A^TA \in \mathbb{M}_{n \times n}(\mathbb{R})\) (chacune est répétée autant de fois que sa multiplicité algébrique), en distinguant ses valeurs propres positives \(\lambda_1 \geqslant \dots \geqslant \lambda_\ell \gt 0\), où \(\ell = \mathrm{rang}(A) = \mathrm{rang}(A^T A)\).
Les valeurs singulières de \(A\) sont
\[
\sigma_j := \sqrt{\lambda_j}\,,\qquad j=1,2,\dots,\ell\,.
\]
La matrice \(\Sigma \in \mathbb{M}_{m \times n}(\mathbb{R})\) s'obtient alors
\[
\Sigma :=
\left[\begin{array}{cc}
\begin{array}{ccc}
\sigma_1 & \cdots & 0
\\
\vdots & \ddots & \vdots
\\
0 & \cdots & \sigma_\ell
\end{array}
&\mathbf{0}\\
\mathbf{0}&\mathbf{0}
\end{array}
\right]_{\square}\,.
\]
- (SVD.2) Une base orthonormée \(\{\boldsymbol{v}_1, \dots, \boldsymbol{v}_n\}\) de vecteurs propres de \(A^TA\), où \(\boldsymbol{v}_i\) est le vecteur propre de valeur propre \(\lambda_i\), donnent la matrice
\[
V := [\boldsymbol{v}_1 \hskip 0.6mm \cdots \hskip 0.6mm \boldsymbol{v}_n] \in \mathbb{M}_{n \times n}(\mathbb{R})\,,
\]
les \(n-\ell\) dernières colonnes étant
associées à la valeur propre nulle (si besoin est).
- (SVD.3) On définit d'abord
\[
\boldsymbol{u}_j:= \tfrac{1}{\sqrt{\lambda_j}}A\boldsymbol{v}_j\,,\qquad j=1,2,\dots,\ell\,.
\]
Si \(\ell = m\), on pose
\[
U := [\boldsymbol{u}_1 \hskip 0.6mm \cdots \hskip 0.6mm \boldsymbol{u}_m] \in \mathbb{M}_{m \times m}(\mathbb{R})\,.
\]
Si \(\ell < m\), on utilise une entre les deux méthodes ci-dessous:
- (SVD.3.i) on complète
\(\{\boldsymbol{u}_1,\dots,\boldsymbol{u}_\ell\}\)
en une base \(\{\boldsymbol{u}_1,\dots,\boldsymbol{u}_\ell,\boldsymbol{w}_{\ell+1},\dots,\boldsymbol{w}_m\}\) de \(\mathbb{R}^m\), et on applique le procédé d'orthonormalisation de Gram-Schmidt pour obtenir une base orthonormée
\(\{\boldsymbol{u}_1,\dots,\boldsymbol{u}_\ell,\boldsymbol{u}_{\ell+1},\dots,\boldsymbol{u}_m\}\) de \(\mathbb{R}^m\);
- (SVD.3.ii) on calcule une base \(\{\boldsymbol{w}_{\ell+1},\dots,\boldsymbol{w}_m\}\) du noyau de la matrice \(A^T \in \mathbb{M}_{n \times m}(\mathbb{R})\) (ou \(AA^T \in \mathbb{M}_{m \times m}(\mathbb{R})\)), et on applique le procédé d'orthonormalisation de Gram-Schmidt pour obtenir une base orthonormée
\(\{\boldsymbol{u}_{\ell+1},\dots,\boldsymbol{u}_m\}\) de \(\mathrm{Ker}(A^T) = \mathrm{Ker}(AA^T) \subseteq \mathbb{R}^m\).
On pose finalement
\[
U := [\boldsymbol{u}_1 \hskip 0.6mm \cdots \hskip 0.6mm \boldsymbol{u}_\ell \hskip 0.6mm \boldsymbol{u}_{\ell+1} \hskip 0.6mm \cdots \hskip 0.6mm \boldsymbol{u}_m] \in \mathbb{M}_{m \times m}(\mathbb{R})\,.
\]
Remarque:
Le calcul des premiers \(\boldsymbol{u}_j\) peut également se faire comme suit:
\[
\boldsymbol{u}_j:= \tfrac{1}{\|A\boldsymbol{v}_j\|}A\boldsymbol{v}_j\,,\qquad j=1,2,\dots,\ell\,.
\]
En effet, par un calcul que l'on a déjà fait,
\[\begin{aligned}
\|A\boldsymbol{v}_j\|^2
&=(A\boldsymbol{v}_j)\cdotp(A\boldsymbol{v}_j)
=\boldsymbol{v}_j\cdotp(A^TA\boldsymbol{v}_j)
=\boldsymbol{v}_j\cdotp(\lambda_j\boldsymbol{v}_j)
=\lambda_j\|\boldsymbol{v}_j\|^2
=\lambda_j\,,
\end{aligned}\]
et donc \(\|A\boldsymbol{v}_j\|=\sqrt{\lambda_j}\).
Remarquons que le travail nécessaire pour diagonaliser \(A^TA\) et \(AA^T\) peut
être très différent, étant donné que ces matrices sont a priori de tailles
différentes!
Exemple:
Calculons la décomposition en valeurs singulières de
\[
A=
\begin{pmatrix}
\frac{3}{2\sqrt{2}}&\frac{1}{2\sqrt{2}}\\
\frac{9}{10\sqrt{2}}&\frac{13}{10\sqrt{2}}
\end{pmatrix}\,.
\]
Comme \(A\) est una matrice de taille \(2\times 2\), sa décomposition \(A=U\Sigma V^T\) sera un
produit de trois matrices de taille \(2\times 2\).
On commence par
calculer \(V\), qui on le rappelle est formée de vecteurs propres de
\(A^TA\). Or
\[\begin{aligned}
A^TA
&=\frac{1}{100}
\begin{pmatrix}
153&96\\
96&97
\end{pmatrix}\,,
\end{aligned}\]
et on sait (voir exercices) que cette dernière possède deux valeurs propres,
\(\lambda_1=9/4\), \(\lambda_2=1/4\), et que les espaces propres associés sont
\[
E_{9/4}=\mathrm{Vect}\left\{ \begin{pmatrix} 4\\ 3 \end{pmatrix} \right\}
\,,\qquad
E_{1/4}=\mathrm{Vect}\left\{ \begin{pmatrix} -3\\ 4 \end{pmatrix} \right\}\,,
\]
qui donne, après normalisation,
\[
E_{9/4}=\mathrm{Vect}\left\{ \begin{pmatrix} 4/5\\ 3/5 \end{pmatrix} \right\}
\,,\qquad
E_{1/4}=\mathrm{Vect}\left\{ \begin{pmatrix} -3/5\\ 4/5 \end{pmatrix} \right\}\,.
\]
On peut donc prendre
\[
V=
\begin{pmatrix}
4/5&-3/5\\
3/5&4/5
\end{pmatrix}\,,
\]
qui correspond à une rotation d'angle \(\theta=\arccos(4/5)\).
Ainsi, \(V^T=V^{-1}\)
correspond à une rotation de \(-\theta\).
Étant connues les valeurs propres de \(A^TA\), les valeurs singulières de \(A\)
sont données par
\[
\sigma_1=\sqrt{\lambda_1}=\frac32\,,\qquad
\sigma_2=\sqrt{\lambda_2}=\frac12\,,
\]
ce qui donne
\[
\Sigma=
\begin{pmatrix} 3/2&0\\ 0&1/2 \end{pmatrix}\,.
\]
Ensuite, \(U\) a pour colonnes des vecteurs propres de \(AA^T\), or
\[ AA^T=
\begin{pmatrix}
5/4&1\\
1&5/4
\end{pmatrix}\,,
\]
qui possède comme valeurs propres
\(\lambda_1=9/4\) et \(\lambda_2=1/4\) (comme on sait, les mêmes que \(A^TA\)!).
Ses espaces propres correspondants sont donnés par
\[
E_{9/4}=\mathrm{Vect}\left\{ \begin{pmatrix} 1\\ 1 \end{pmatrix} \right\}
\,,\qquad
E_{1/4}=\mathrm{Vect}\left\{ \begin{pmatrix} -1\\ 1 \end{pmatrix} \right\}\,,
\]
ou encore, après normalisation:
\[
E_{9/4}=\mathrm{Vect}\left\{ \begin{pmatrix} 1/\sqrt{2}\\ 1/\sqrt{2} \end{pmatrix} \right\}
\,,\qquad
E_{1/4}=\mathrm{Vect}\left\{ \begin{pmatrix} -1/\sqrt{2}\\ 1/\sqrt{2} \end{pmatrix} \right\}\,,
\]
On a donc
\[
U=
\begin{pmatrix}
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}\\
\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}
\end{pmatrix}\,,
\]
qui n'est autre qu'une rotation de \(\phi=\frac{\pi}{4}\).
Remarquons qu'on aurait aussi pu trouver les colonnes de \(U\) en faisant
\[ \boldsymbol{u}_1=\frac{1}{\sigma_1}A\boldsymbol{v}_1
=\frac{1}{3/2}
\begin{pmatrix}
\frac{3}{2\sqrt{2}}&\frac{1}{2\sqrt{2}}\\
\frac{9}{10\sqrt{2}}&\frac{13}{10\sqrt{2}}
\end{pmatrix}
\begin{pmatrix} 4/5\\ 3/5 \end{pmatrix}
=\begin{pmatrix} 1/\sqrt{2}\\ 1/\sqrt{2} \end{pmatrix}\,,
\]
pareil pour \(\boldsymbol{u}_2\).
On a donc la décomposition en valeurs singulières de \(A\), qui permet de
voir la transformation
\[\boldsymbol{x}\mapsto A\boldsymbol{x}=
\underbrace{
{\color{green}
\begin{pmatrix}
1/\sqrt{2}&-1/\sqrt{2}\\
1/\sqrt{2}&1/\sqrt{2}
\end{pmatrix}
}
\underbrace{
{\color{blue}
\begin{pmatrix} 3/2&0\\ 0&1/2 \end{pmatrix}
}
\underbrace{
{\color{magenta}
\begin{pmatrix}
4/5&3/5\\
-3/5&4/5
\end{pmatrix}
}
\boldsymbol{x}
}_{V^T\boldsymbol{x}}
}_{\Sigma V^T\boldsymbol{x}}
}_{U\Sigma V^T\boldsymbol{x}}
\,.
\]
comme une composition
- d'une
\({\color{magenta}\text{rotation}}\) d'angle \(-\theta\simeq -36.9^o\), suivie
- d'un
\({\color{blue}\text{étirement}}\) le long des axes de coordonnées (\(3/2\) selon
\(\boldsymbol{e}_1\), \(1/2\) selon \(\boldsymbol{e}_2\)), suivi
- d'une \({\color{green}\text{rotation}}\) d'angle \(\phi=+45^o\).
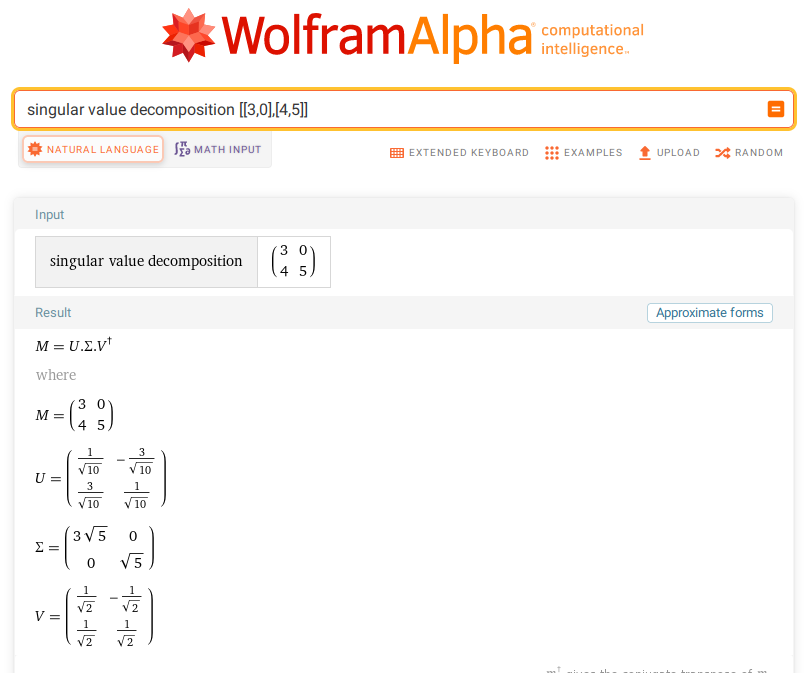
Remarque:
Wolfram Alpha
peut donner une
décomposition en valeurs singulières de n'importe quelle matrice.
Par exemple, pour obtenir la décomposition de
\[ M=
\begin{pmatrix}
3&0\\
4&5
\end{pmatrix}\,,
\]
il suffit d'entrer
''singular value decomposition \([[3,0],[4,5]]\)''
Exemple:
Calculons la décomposition en valeurs singulières de
\[
A=
\begin{pmatrix}
1&1\\
1&1\\
0&0
\end{pmatrix}\,.
\]
On commence par
\[
A^TA=
\begin{pmatrix}
2&2\\
2&2
\end{pmatrix}\,,
\]
qui possède deux valeurs propres, \(\lambda_1=4\) et \(\lambda_2=0\).
Ainsi, \(A\) possède une seule valeur singulière non-nulle:
\(\sigma_1=\sqrt{\lambda_1}=2\).
On trouve un vecteur propre unitaire pour chaque valeur propre, par exemple:
\[
\boldsymbol{v}_1=
\begin{pmatrix} 1/\sqrt{2}\\ 1/\sqrt{2} \end{pmatrix}\,,
\qquad
\boldsymbol{v}_2=
\begin{pmatrix} -1/\sqrt{2}\\ 1/\sqrt{2} \end{pmatrix}\,,
\]
qui donne déjà
\[
V=
\begin{pmatrix}
1/\sqrt{2}& -1/\sqrt{2}\\
1/\sqrt{2}& 1/\sqrt{2}
\end{pmatrix}\,,
\]
Pour calculer \(U\), on peut soit passer par l'étude de \(AA^T\), ou alors
commencer par obtenir une de ses colonnes en prenant
\[ \boldsymbol{u}_1=\frac{1}{\sqrt{\lambda_1}}A\boldsymbol{v}_1=\frac{1}{2}
\begin{pmatrix}
1&1\\
1&1\\
0&0
\end{pmatrix}
\begin{pmatrix} 1/\sqrt{2}\\ 1/\sqrt{2} \end{pmatrix}
=
\begin{pmatrix} 1/\sqrt{2}\\ 1/\sqrt{2}\\ 0 \end{pmatrix}\,.
\]
On doit maintenant trouver deux colonnes \(\boldsymbol{u}_2\) et \(\boldsymbol{u}_3\), de
façon à ce que \(U=[\boldsymbol{u}_1\,\boldsymbol{u}_2\,\boldsymbol{u}_3]\) soit orthogonale.
On peut par exemple prendre
\[
\boldsymbol{u}_2=
\begin{pmatrix}
1/\sqrt{2}\\
-1/\sqrt{2}\\
0
\end{pmatrix}
\,,\qquad
\boldsymbol{u}_3=
\begin{pmatrix}
0\\
0\\
1
\end{pmatrix}\,.
\]
Il reste à produire \(\Sigma\). Puisque \(A\) n'a qu'une seule valeur singulière
non-nulle,
et que \(\Sigma\) doit être de taille \(3\times 2\), on rajoute des blocs
appropriés:
\[ \Sigma=
\begin{pmatrix}
2&{\color{orange}0}\\
{\color{purple}0}&{\color{teal}0}\\
{\color{purple}0}&{\color{teal}0}\\
\end{pmatrix}\,.
\]
On a donc une décomposition en valeurs singulières pour \(A\):
\[\begin{aligned}
A&=
\begin{pmatrix}
1&1\\
1&1\\
0&0
\end{pmatrix}\\
&=
\begin{pmatrix}
1/\sqrt{2}&1/\sqrt{2}&0\\
1/\sqrt{2}&-1/\sqrt{2}&0\\
0&0&1
\end{pmatrix}
\begin{pmatrix}
2&{\color{orange}0}\\
{\color{purple}0}&{\color{teal}0}\\
{\color{purple}0}&{\color{teal}0}\\
\end{pmatrix}
\begin{pmatrix}
1/\sqrt{2}& -1/\sqrt{2}\\
1/\sqrt{2}& 1/\sqrt{2}
\end{pmatrix}^T\,,
\end{aligned}\]
Exemple:
Étudions la décomposition en valeurs singulières de
\[
A=
\begin{pmatrix}
3&1&1\\
-1&3&1
\end{pmatrix}\,,
\]
pour laquelle on aura une matrice \(U\) de taille \(2\times 2\), une matrice
\(\Sigma\) de taille \(2\times 3\) et une matrice \(V\) de taille \(3\times 3\).
Commençons par
\[
A^TA=
\begin{pmatrix}
10&0&2\\
0&10&4\\
2&4&2
\end{pmatrix}\,,
\]
qui a pour polynôme caractéristique
\[
P_{A^TA}(\lambda)
=-\lambda(\lambda-10)(\lambda-12)\,.
\]
On a donc les valeurs propres, en ordre décroissant,
\(\lambda_1=12\),
\(\lambda_2=10\),
\(\lambda_3=0\). On a donc deux valeurs singulières strictement positives,
\(\sigma_1=\sqrt{12}=2\sqrt{3}\), \(\sigma_2=\sqrt{10}\).
Les espaces propres sont:
\[
E_{12}=\mathrm{Ker}(A^TA-12 I_3)=\mathrm{Vect}\left\{
\begin{pmatrix} 1\\ 2\\ 1 \end{pmatrix}
\right\}\,,
\]
\[
E_{10}=\mathrm{Ker}(A^TA-10 I_3)=\mathrm{Vect}\left\{
\begin{pmatrix} -2\\ 1\\0 \end{pmatrix}
\right\}\,,
\]
\[
E_{0}=\mathrm{Ker}(A^TA)=\mathrm{Ker}(A)=\mathrm{Vect}\left\{
\begin{pmatrix} -1\\ -2\\5 \end{pmatrix}
\right\}\,.
\]
On peut donc normaliser et obtenir
\[
V=[\boldsymbol{v}_1\,\boldsymbol{v}_2\,\boldsymbol{v}_3]
=
\begin{pmatrix}
1/\sqrt{6}&-2/\sqrt{5}&-1/\sqrt{30}\\
2/\sqrt{6}&1/\sqrt{5}&-2/\sqrt{30}\\
1/\sqrt{6}&0&5/\sqrt{30}
\end{pmatrix}\,.
\]
La matrice \(U=[\boldsymbol{u}_1\,\boldsymbol{u}_2]\) s'obtient par
\[
\boldsymbol{u}_1=\frac{1}{\sigma_1}A\boldsymbol{v}_1=
\frac{1}{2\sqrt{3}}
\begin{pmatrix}
3&1&1\\
-1&3&1
\end{pmatrix}
\begin{pmatrix} 1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6} \end{pmatrix}
=
\begin{pmatrix}
1/\sqrt{2}\\
1/\sqrt{2}
\end{pmatrix}\,,
\]
\[
\boldsymbol{u}_2=\frac{1}{\sigma_2}A\boldsymbol{v}_2=
\frac{1}{\sqrt{10}}
\begin{pmatrix}
3&1&1\\
-1&3&1
\end{pmatrix}
\begin{pmatrix} -2/\sqrt{5}\\ 1/\sqrt{5}\\ 0 \end{pmatrix}
=
\begin{pmatrix}
-1/\sqrt{2}\\
1/\sqrt{2}
\end{pmatrix}\,.
\]
Finalement, les deux valeurs singulières positives
permettent d'écrire
\[
\Sigma=
\begin{pmatrix}
2\sqrt{3}&0&{\color{orange}0}\\
0&\sqrt{10}&{\color{orange}0}
\end{pmatrix}\,.
\]
On a donc une décomposition en valeurs singulières pour \(A\):
\[\begin{aligned}
A&=
\begin{pmatrix}
3&1&1\\
-1&3&1
\end{pmatrix}\\
&=
\begin{pmatrix}
1/\sqrt{2}&-1/\sqrt{2}\\
1/\sqrt{2}&1/\sqrt{2}\\
\end{pmatrix}
\begin{pmatrix}
2\sqrt{3}&0&{\color{orange}0}\\
0&\sqrt{10}&{\color{orange}0}
\end{pmatrix}
\begin{pmatrix}
1/\sqrt{6}&-2/\sqrt{5}&-1/\sqrt{30}\\
2/\sqrt{6}&1/\sqrt{5}&-2/\sqrt{30}\\
1/\sqrt{6}&0&5/\sqrt{30}
\end{pmatrix}^T\,.
\end{aligned}\]