Analyse réelle | S. Friedli

Considérons deux espaces vectoriels, \(V\) et \(V'\), ainsi qu'une application linéaire \(T:V\to V'\).

Supposons maintenant que ces deux espaces vectoriels sont tous deux de dimension finie, chacun muni d'une base:

Nous allons voir maintenant comment l'utilisation de ces bases va permettre de ramener l'étude de \(T\) à l'étude d'une application linéaire de \(\mathbb{R}^p\) dans \(\mathbb{R}^m\).

En effet, prenons un vecteur dans l'ensemble de départ, \(v\in V\), et décomposons-le sur \(\mathcal{B}\): \[v=a_1v_1+\dots+a_pv_p\,,\] ce qui permet de décrire \(v\) univoquement à l'aide du vecteur de \(\mathbb{R}^p\) qui lui est associé: \[ [v]_\mathcal{B} = \begin{pmatrix} a_1\\ \vdots\\ a_p \end{pmatrix} \,. \] Ensuite, regardons l'image de \(v\) par \(T\). Puisque \(T\) est linéaire, \[\begin{aligned} T(v) &=T(a_1v_1+\dots+a_pv_p)\\ &=a_1T(v_1)+\dots+a_pT(v_p)\,. \end{aligned}\] En utilisant ensuite la linéarité de \([\cdot]_{\mathcal{B}'}\), \[\begin{aligned} [T(v)]_{\mathcal{B}'} &=\bigl[a_1T(v_1)+\dots+a_pT(v_p)\bigr]_{\mathcal{B}'}\\ &=a_1[T(v_1)]_{\mathcal{B}'}+\dots+a_p[T(v_p)]_{\mathcal{B}'}\,. \end{aligned}\] Cette dernière ligne est une combinaison linéaire des vecteurs \([T(v_1)]_{\mathcal{B}'},\cdots,[T(v_p)]_{\mathcal{B}'}\) de \(\mathbb{R}^m\), on peut donc l'interpréter comme un produit d'une matrice par le vecteur \([v]_{\mathcal{B}}\): \[\begin{aligned} a_1[T(v_1)]_{\mathcal{B}'}+\dots+a_p[T(v_p)]_{\mathcal{B}'} &= \underbrace{\bigl[[T(v_1)]_{\mathcal{B}'} \cdots [T(v_p)]_{\mathcal{B}'}\bigr]}_{m\times n} \underbrace{\begin{pmatrix} a_1\\ \vdots\\ a_p \end{pmatrix}}_{=[v]_{\mathcal{B}}}\\ &= \bigl[[T(v_1)]_{\mathcal{B}'} \cdots [T(v_p)]_{\mathcal{B}'}\bigr] [v]_\mathcal{B} \end{aligned}\]

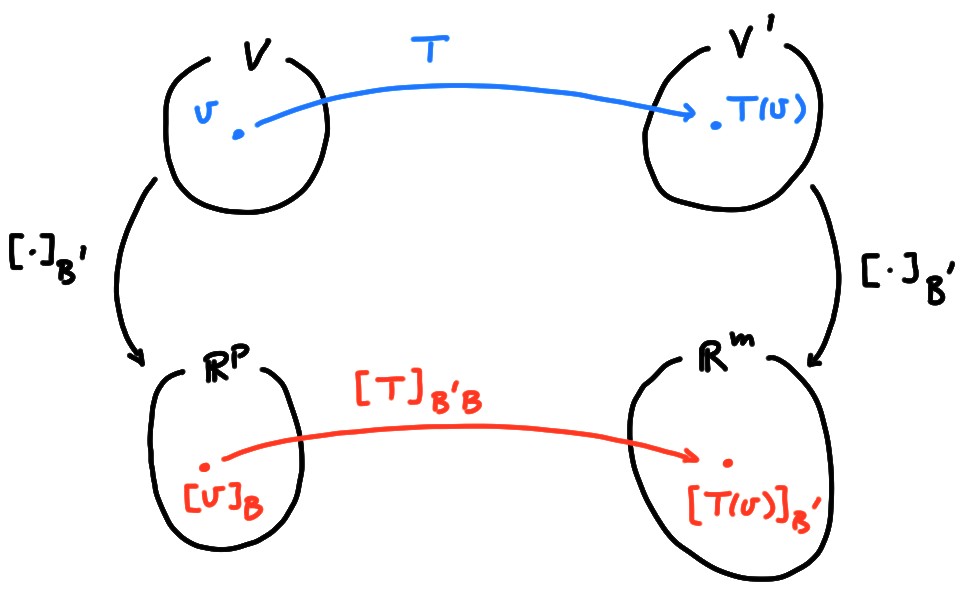
En utilisant les bases \(\mathcal{B}\) et \(\mathcal{B}'\), ainsi que les applications \([\cdot]_{\mathcal{B}}\) et \([\cdot]_{\mathcal{B}'}\) qui leur sont associées, nous avons pu prendre l'application \[{\color{blue}v\mapsto T(v)}\,\] qui est abstraite, et nous l'avons rendue plus concrète, en la représentant à l'aide d'une matrice: on peut maintenant la voir comme une application linéaire de \(\mathbb{R}^p\) dans \(\mathbb{R}^m\), dont la matrice est \([T]_{\mathcal{B}'\mathcal{B}}\): \[ \underbrace{{\color{red}[v]_\mathcal{B}}}_{\in \mathbb{R}^p} \,\, {\color{red}\mapsto} \,\, \underbrace{{\color{red}[T(v)]_{\mathcal{B}'}}}_{\in \mathbb{R}^m} = {\color{red} [T]_{\mathcal{B}'\mathcal{B}} [v]_\mathcal{B} } \] Maintenant, l'étude de \(T\) peut se réduire à celle de la matrice \([T]_{\mathcal{B}'\mathcal{B}}\).

Exemple: Considérons l'application \(T:\mathbb{P}_3\to \mathbb{P}_2\) définie ainsi: pour \(p\in \mathbb{P}_3\), \[ T(p)=p'\,, \] qui signifie que \(T(p)(t):= p'(t)\) (dérivée de \(p\) par rapport à \(t\)).

Cette application est clairement linéaire puisque \[ T(\alpha p+\beta q)=(\alpha p+\beta q)'=\alpha p'+\beta q'= \alpha T(p)+\beta T(q)\,. \] Calculons maintenant la matrice associée à cette application, relativement

à la base canonique \(\mathcal{B}_{\mathrm{can}}=(e_0,e_1,e_2,e_3)\) dans \(\mathbb{P}_3\), et
à la base canonique \(\mathcal{B}_{\mathrm{can}}'=(e_0,e_1,e_2)\) dans \(\mathbb{P}_2\).

Par ce qu'on a dit plus haut, cette matrice sera \[ [T]_{\mathcal{B}_{\mathrm{can}}'\mathcal{B}_{\mathrm{can}}} = \bigl[[T(e_0)]_{\mathcal{B}_{\mathrm{can}}'}\,[T(e_1)]_{\mathcal{B}_{\mathrm{can}}'}\,[T(e_2)]_{\mathcal{B}_{\mathrm{can}}'} \,[T(e_3)]_{\mathcal{B}_{\mathrm{can}}'}\bigr]\,. \] Comme \[ e_0(t)=1\,\quad e_1(t)=t\,\quad e_2(t)=t^2\,\quad e_3(t)=t^3\,, \] on a \[ e_0'(t)=0\,\quad e_1'(t)=1\,\quad e_2'(t)=2t\,\quad e_3'(t)=3t^2\,, \] et donc \[ T(e_0)=0\,,\qquad T(e_1)=e_0\,,\qquad T(e_2)=2e_1\,,\qquad T(e_3)=3e_2\,, \] c'est-à-dire \[\begin{aligned} T(e_0)&=0 e_0+0e_1 + 0e_2\\ T(e_1)&=1 e_0+0e_1 + 0e_2\\ T(e_2)&=0 e_0+2e_1 + 0e_2\\ T(e_3)&=0 e_0+0e_1 + 3e_2\,. \end{aligned}\] On peut donc écrire \[\begin{aligned} [T(e_0)]_{\mathcal{B}_{\mathrm{can}}'}&= \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \,,\qquad [T(e_1)]_{\mathcal{B}_{\mathrm{can}}'}= \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}\\ [T(e_2)]_{\mathcal{B}_{\mathrm{can}}'}&= \begin{pmatrix} 0\\ 2\\ 0 \end{pmatrix} \,,\qquad [T(e_3)]_{\mathcal{B}_{\mathrm{can}}'}= \begin{pmatrix} 0\\ 0\\ 3 \end{pmatrix} \end{aligned}\] La matrice qui représente \(T\) est donc, relativement à ce choix de bases, \[ [T]_{\mathcal{B}_{\mathrm{can}}'\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3 \end{pmatrix} \] Prenons par exemple le polynôme \(p\in \mathbb{P}_3\) défini par \[ p(t)=2+t^2-5t^3\,, \] pour lequel \[ [p]_{\mathcal{B}_{\mathrm{can}}} = \begin{pmatrix} 2\\ 0\\ 1\\ -5 \end{pmatrix}\,. \] Son image par \(T\) est \(T(p)\in \mathbb{P}_2\), qui relativement à \(\mathcal{B}_{\mathrm{can}}'\) est donnée par \[ [T(p)]_{\mathcal{B}_{\mathrm{can}}'}= [T]_{\mathcal{B}_{\mathrm{can}}'\mathcal{B}_{\mathrm{can}}} [p]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 0&1&0&0\\ 0&0&2&0\\ 0&0&0&3 \end{pmatrix} \begin{pmatrix} 2\\ 0\\ 1\\ -5 \end{pmatrix} = \begin{pmatrix} 0\\ 2\\ -15 \end{pmatrix}\,, \] qui est bien la décomposition de \[p'(t)=(2+t^2-5t^3)'=2t-15t^2 \] relativement à \(\mathcal{B}_{\mathrm{can}}'\): \[ [p']_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 0\\ 2\\ -15 \end{pmatrix}\,. \]

Exemple: Considérons l'application \[\begin{aligned} T:\mathbb{P}_2&\to\mathbb{R}^2\\ p&\mapsto T(p):= \begin{pmatrix} p(0)\\p'(1) \\ \end{pmatrix}\,. \end{aligned}\] (\(p'(t)\) est la dérivée de \(p(t)\) par rapport à \(t\).) Remarquons que \(T\) est linéaire, puisque pour tous \(p,q\in \mathbb{P}_2\) et tout scalaires \(\alpha,\beta\), \[\begin{aligned} T(\alpha p+\beta q) &= \begin{pmatrix} \alpha p(0)+\beta q(0)\\ \alpha p'(1)+\beta q'(1) \end{pmatrix}\\ &= \alpha \begin{pmatrix} p(0)\\ p'(1) \end{pmatrix} + \beta \begin{pmatrix} q(0)\\ q'(1) \end{pmatrix} =\alpha T(p)+\beta T(q)\,. \end{aligned}\] Puisqu'on connaît la base canonique \(\mathcal{B}_{\mathrm{can}}=(e_0,e_1,e_2)\) dans \(\mathbb{P}_2\) et la base canonique \(\mathcal{B}_{\mathrm{can}}'=(\boldsymbol{e}_1,\boldsymbol{e}_2)\) dans \(\mathbb{R}^2\) (on écrit \(\mathcal{B}_{\mathrm{can}}'\) juste pour la distinguer de l'autre, mais c'est bien la base canonique de \(\mathbb{R}^2\)), on peut calculer la matrice \(2\times 3\) qui représente \(T\) relativement à ces bases: \[ [T]_{\mathcal{B}_{\mathrm{can}}'\mathcal{B}_{\mathrm{can}}} = \bigl[[T(e_0)]_{\mathcal{B}_{\mathrm{can}}'}\,[T(e_1)]_{\mathcal{B}_{\mathrm{can}}'}\,[T(e_2)]_{\mathcal{B}_{\mathrm{can}}'}\bigr]\,. \] Comme \(e_0(t)=1\), \(e_1(t)=t\), \(e_2(t)=t^2\), on a \[\begin{aligned} T(e_0)&= \begin{pmatrix} e_0(0)\\ e_0'(1) \end{pmatrix} = \begin{pmatrix} 1\\ 0 \end{pmatrix}\\ T(e_1)&= \begin{pmatrix} e_1(0)\\ e_1'(1) \end{pmatrix} = \begin{pmatrix} 0\\ 1\end{pmatrix}\\ T(e_2)&= \begin{pmatrix} e_2(0)\\ e_2'(1) \end{pmatrix} = \begin{pmatrix} 0\\ 2\end{pmatrix}\,, \end{aligned}\] et donc \[ [T]_{\mathcal{B}_{\mathrm{can}}'\mathcal{B}_{\mathrm{can}}} = \begin{pmatrix} 1&0&0\\ 0&1&2 \end{pmatrix}\,. \] Par exemple, prenons le polynôme \(p(t)=9-2t+7t^2\), et calculons son image. Alors \[\begin{aligned} [T(p)]_{\mathcal{B}_{\mathrm{can}}'} &= [T]_{\mathcal{B}_{\mathrm{can}}'\mathcal{B}_{\mathrm{can}}}[p]_{\mathcal{B}_{\mathrm{can}}}\\ &= \begin{pmatrix} 1&0&0\\ 0&1&2 \end{pmatrix} \begin{pmatrix} 9\\ -2\\ 7 \end{pmatrix} = \begin{pmatrix} 9\\12 \end{pmatrix}\,, \end{aligned}\] qui est bien \( \begin{pmatrix} p(0)\\p'(1) \end{pmatrix} \).

Nous reviendrons plus en profondeur sur la représentation d'une application linéaire à l'aide d'une matrice, en particulier dans le cas \(T:\mathbb{R}^n\to\mathbb{R}^m\).

Quiz 4.8-1 : Soient \(V\) et \(V'\) deux espaces vectoriels de dimensions finies, \(\dim(V)=k\), \(\dim(V')=l\), et soit \(T:V\to V'\) une application. Vrai ou faux?

\(V=\mathbb{R}^k\) et \(V'=\mathbb{R}^l\)
\(V=\mathbb{R}^l\) et \(V'=\mathbb{R}^k\)
\(T\) peut être représentée par une matrice.
Si \(T\) est linéaire, alors la matrice qui la représente est \(k\times l\).
Si \(T\) est linéaire, alors la matrice qui la représente est \(l\times k\).
Si \(\mathcal{B}\) est une base de \(V\) et \(\mathcal{B}'\) est une base de \(V'\), alors la matrice qui représente \(T\) relativement à \(\mathcal{B}\) et \(\mathcal{B}'\) se note \([T]_{\mathcal{B}'\mathcal{B}}\).
Si \(\mathcal{B}\) est une base de \(V\) et \(\mathcal{B}'\) est une base de \(V'\), alors la matrice qui représente \(T\) relativement à \(\mathcal{B}\) et \(\mathcal{B}'\) se note \([T]_{\mathcal{B}\mathcal{B}'}\).

4.8 Matrice d'une application