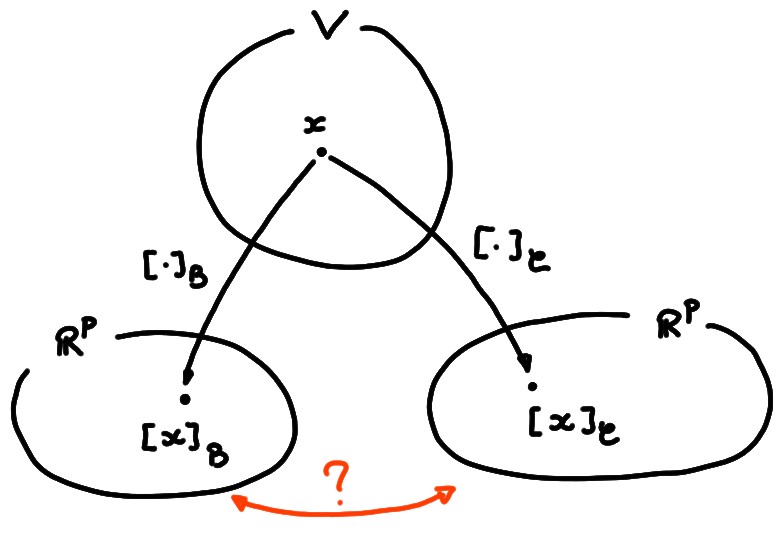
8.2 Effet sur les composantes des vecteurs
Pour commencer, étudions les relations existant entre les composantes d'un
même vecteur, exprimé relativement à une base ou à une autre.
Avant de voir l'approche dans le cas général,
commençons par un exemple simple.
Exemple:
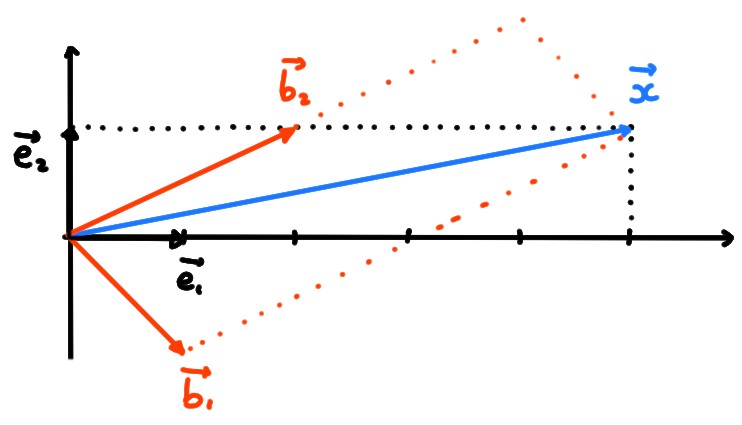
Dans le plan, considérons le vecteur
\[
\boldsymbol{x}= \begin{pmatrix} 5\\ 1 \end{pmatrix}\,.
\]
Considérons maintenant la base \(\mathcal{B}=(\boldsymbol{b}_1,\boldsymbol{b}_2)\), dont les
vecteurs sont disons
\[
\boldsymbol{b}_1= \begin{pmatrix} 1\\-1 \end{pmatrix}\,,\qquad
\boldsymbol{b}_2= \begin{pmatrix} 2\\1 \end{pmatrix}\,.
\]
Quelles sont les composantes de \(\boldsymbol{x}\) relativement à \(\mathcal{B}\)?
Ce qu'on cherche ici est
\[ [\boldsymbol{x}]_\mathcal{B}=
\begin{pmatrix}\beta_1 \\\beta_2 \end{pmatrix}\,,
\]
qui ne signifie rien d'autre que
\[ \boldsymbol{x}=\beta_1\boldsymbol{b}_1+\beta_2\boldsymbol{b}_2\,.
\]
Or cette dernière s'exprime comme
\[
\begin{pmatrix} 5\\1 \end{pmatrix}
=
\beta_1
\begin{pmatrix} 1\\-1 \end{pmatrix}
+\beta_2
\begin{pmatrix} 2\\1 \end{pmatrix}\,,
\]
qui est équivalent au système
\[
\left\{
\begin{array}{ccccc}
\beta_1 &+& 2\beta_2 &=& 5\\
-\beta_1 &+& \beta_2 &=&1
\end{array}
\right.\,,
\]
dont la solution est \(\beta_1=1\), \(\beta_2=2\).
Ainsi,
\[ [\boldsymbol{x}]_\mathcal{B}=
\begin{pmatrix}1 \\2 \end{pmatrix}\,,
\]
qui signifie \(\boldsymbol{x}=\boldsymbol{b}_1+2\boldsymbol{b}_2\).
Remarque: Il est plus utile de penser que \(\boldsymbol{x}\) est un vecteur dans
le plan, et que ce vecteur peut être représenté en composantes, relativement à
la base canonique \(\mathcal{B}_{\mathrm{can}}\) ou à la base \(\mathcal{B}\):
\[
[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}=
\begin{pmatrix}5 \\1 \end{pmatrix}\,,
\qquad
[\boldsymbol{x}]_\mathcal{B}=
\begin{pmatrix}1 \\2 \end{pmatrix}\,.
\]
Bien-sûr, il serait intéressant d'avoir un procédé permettant d'obtenir
directement les composantes d'un vecteur quelconque dans une base, en fonction
des composantes dans l'autre base:
\[
[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}=
\begin{pmatrix}\gamma_1 \\\gamma_2 \end{pmatrix}
\overset{?}{\longleftrightarrow}
\begin{pmatrix}\beta_1 \\\beta_2 \end{pmatrix}
=[\boldsymbol{x}]_\mathcal{B}
\]
La matrice de changement de base
Abordons le problème d'un point de vue général.
Soit \(V\) un espace vectoriel de dimension \(p\).
Supposons que l'on ait deux bases dans \(V\):
\[
\mathcal{B}=(b_1,\dots,b_p)\,,\qquad \mathcal{C}=(c_1,\dots,c_p)\,.
\]
Si \(x\in V\) est un vecteur quelconque, il peut être décomposé dans une base ou
dans l'autre, et les composantes relativement à ces bases seront a priori
différentes:
\[
[x]_\mathcal{B}=
\begin{pmatrix}
\beta_1\\
\vdots\\
\beta_p
\end{pmatrix}\,,
\qquad
[x]_\mathcal{C}=
\begin{pmatrix}
\gamma_1\\
\vdots\\
\gamma_p
\end{pmatrix}\,.
\]
Nous aimerions savoir comment les composantes relativement à
une base, par exemple les
\(\beta_1,\dots,\beta_p\), peuvent se calculer à partir des composantes dans
l'autre base, c'est-à-dire les \(\gamma_1,\dots,\gamma_p\).
Nous allons voir que cette relation est linéaire, et peut donc s'exprimer à
l'aide d'une matrice:
Théorème:
Il existe une matrice \(p\times p\), notée \(P_{\mathcal{C}\mathcal{B}}\) (ou parfois:
\(P_{\mathcal{C}\leftarrow \mathcal{B}}\)), telle que
\[
[x]_\mathcal{C}=P_{\mathcal{C}\mathcal{B}}[x]_\mathcal{B}\,.
\]
De plus,
- \(P_{\mathcal{C}\mathcal{B}}=\bigl[[b_1]_\mathcal{C}\cdots [b_p]_\mathcal{C}\bigr]\),
- \(P_{\mathcal{C}\mathcal{B}}\) est inversible, et
\({P_{\mathcal{C}\mathcal{B}}}^{-1}=P_{\mathcal{B}\mathcal{C}}\).
On appelle \(P_{\mathcal{C}\mathcal{B}}\) la
matrice de changement de base de \(\mathcal{B}\) vers \(\mathcal{C}\).
Preuve:
\[\begin{aligned}
[x]_\mathcal{C}
&=\bigl[\beta_1b_1+\dots+\beta_pb_p\bigr]_{\mathcal{C}}\\
&=\beta_1[b_1]_\mathcal{C}+\dots+\beta_p[b_p]_\mathcal{C}\\
&=\bigl[[b_1]_\mathcal{C}\cdots [b_p]_\mathcal{C}\bigr]
\begin{pmatrix} \beta_1\\ \vdots\\ \beta_p \end{pmatrix}\\
&=P_{\mathcal{C}\mathcal{B}}[x]_{\mathcal{B}}
\end{aligned}\]
En procédant dans l'autre sens, on obtient
\[\begin{aligned}
[x]_\mathcal{B}
&=\bigl[\gamma_1 c_1+\dots+\gamma_p c_p\bigr]_{\mathcal{B}}\\
&=\gamma_1[c_1]_\mathcal{C}+\dots+\gamma_p[c_p]_\mathcal{B}\\
&=\bigl[[c_1]_\mathcal{B}\cdots [c_p]_\mathcal{B}\bigr]
\begin{pmatrix} \gamma_1\\ \vdots\\ \gamma_p \end{pmatrix}\\
&=P_{\mathcal{B}\mathcal{C}}[x]_{\mathcal{C}}
\end{aligned}\]
Si on réinjecte cette dernière dans celle du dessus,
\[\begin{aligned}
[x]_\mathcal{C}
&=P_{\mathcal{C}\mathcal{B}}[x]_\mathcal{B}\\
&=P_{\mathcal{C}\mathcal{B}}P_{\mathcal{B}\mathcal{C}}[x]_\mathcal{C}\,.
\end{aligned}\]
Comme cette dernière est vraie pour tout \(x\in V\), on a
\[P_{\mathcal{C}\mathcal{B}}P_{\mathcal{B}\mathcal{C}}=I_p\,.\]
Donc \(P_{\mathcal{C}\mathcal{B}}\) est
inversible, et son inverse est
\({P_{\mathcal{C}\mathcal{B}}}^{-1}=P_{\mathcal{B}\mathcal{C}}\).
Remarque:
En bas de page, on explique pourquoi la matrice de changement de base n'est que
la représentation de l'application
linéaire identité, de \(V\) dans lui-même.
Exemple:
Dans le plan, considérons comme tout à l'heure le vecteur
\[
\boldsymbol{x}= \begin{pmatrix} 5\\ 1 \end{pmatrix}\,.
\]
Pour être plus précis, notons \(\mathcal{B}_{\mathrm{can}}=(\boldsymbol{e}_1,\boldsymbol{e}_2)\) la base canonique,
et récrivons
\[
[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 5\\ 1 \end{pmatrix}\,.
\]
Considérons maintenant la base \(\mathcal{B}=(\boldsymbol{b}_1,\boldsymbol{b}_2)\) définie par:
\[
\boldsymbol{b}_1= \begin{pmatrix} 1\\-1 \end{pmatrix}\,,\qquad
\boldsymbol{b}_2= \begin{pmatrix} 2\\1 \end{pmatrix}\,.
\]
Calculons \([\boldsymbol{x}]_\mathcal{B}\), en fonction de
\([\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}\), en utilisant le théorème:
\[
[
\boldsymbol{x}]_\mathcal{B} =P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}} [\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}} \,,
\]
où
\[P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}=\bigl[[\boldsymbol{e}_1]_\mathcal{B}\,[\boldsymbol{e}_2]_\mathcal{B}\bigr]\,.\]
On doit donc
trouver les composantes de \(\boldsymbol{e}_1\) et \(\boldsymbol{e}_2\) relativement
à \(\mathcal{B}\). Mais comme
\[
[\boldsymbol{b}_1]_{\mathcal{B}_{\mathrm{can}}}=\begin{pmatrix} 1\\-1 \end{pmatrix}\,,\qquad
[\boldsymbol{b}_2]_{\mathcal{B}_{\mathrm{can}}}=\begin{pmatrix} 2\\1 \end{pmatrix}\,
\]
signifie en fait
\[
\left\{
\begin{array}{ccccc}
\boldsymbol{b}_1&=&\boldsymbol{e}_1&-&\boldsymbol{e}_2 \\
\boldsymbol{b}_2&=&2\boldsymbol{e}_1&+&\boldsymbol{e}_2 \,,
\end{array}
\right.
\]
on a
\[
\left\{
\begin{array}{ccccc}
\boldsymbol{e}_1&=&\frac13\boldsymbol{b}_1&+&\frac13\boldsymbol{b}_2 \\
\boldsymbol{e}_2&=&-\frac23\boldsymbol{b}_1&+&\frac13\boldsymbol{b}_2 \,,
\end{array}
\right.
\]
Ainsi,
\[
[\boldsymbol{e}_1]_\mathcal{B}= \begin{pmatrix} 1/3\\ 1/3 \end{pmatrix} \,,\qquad
[\boldsymbol{e}_2]_\mathcal{B}= \begin{pmatrix} -2/3\\ 1/3 \end{pmatrix} \,,
\]
et donc
\[
P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}=\bigl[[\boldsymbol{e}_1]_\mathcal{B}\,[\boldsymbol{e}_2]_\mathcal{B}\bigr]
=
\begin{pmatrix}
1/3&-2/3\\
1/3&1/3
\end{pmatrix}
\]
Donc les coordonnées de \(\boldsymbol{x}\) relativement à \(\mathcal{B}\) sont
\[
[\boldsymbol{x}]_\mathcal{B}=P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}=
\begin{pmatrix}
1/3&-2/3\\
1/3&1/3
\end{pmatrix}
\begin{pmatrix} 5\\1 \end{pmatrix}
=
\begin{pmatrix} 1\\2 \end{pmatrix}\,,
\]
comme nous avions trouvé plus haut.
Si maintenant on souhaite plutôt transformer des
composantes relativement à \(\mathcal{B}\) en des composantes relativement à
\(\mathcal{B}_{\mathrm{can}}\), on calcule
\[
P_{\mathcal{B}_{\mathrm{can}}\mathcal{B}}={P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}}^{-1}
=
\frac{1}{1/3}
\begin{pmatrix} 1/3&2/3\\ -1/3&1/3 \end{pmatrix}
=
\begin{pmatrix} 1&2\\ -1&1 \end{pmatrix}\,.
\]
Donc si par exemple on prend \(\boldsymbol{x}\) tel que
\[
[\boldsymbol{x}]_\mathcal{B}=
\begin{pmatrix} 1\\ 2 \end{pmatrix}\,,
\]
alors ses composantes relativement à \(\mathcal{B}_{\mathrm{can}}\) sont, comme on sait déjà,
\[
[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}
= P_{\mathcal{B}_{\mathrm{can}}\mathcal{B}}[\boldsymbol{x}]_\mathcal{B}
=
\begin{pmatrix} 1&2\\ -1&1 \end{pmatrix}
\begin{pmatrix} 1\\ 2 \end{pmatrix}
=\begin{pmatrix} 5\\ 1 \end{pmatrix}\,.
\]
Exemple:
Supposons que l'on considère, dans \(\mathbb{R}^3\), le vecteur
\[ \boldsymbol{x}= \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}\,. \]
Considérons la base de \(\mathbb{R}^3\), \(\mathcal{B}=(\boldsymbol{b}_1,\boldsymbol{b}_2,\boldsymbol{b}_3)\),
dont les vecteurs sont
(on laisse au lecteur le soin de vérifier que \(\mathcal{B}\) est effectivement une
base):
\[
\boldsymbol{b}_1= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}\,,\qquad
\boldsymbol{b}_2= \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix}\,,\qquad
\boldsymbol{b}_3= \begin{pmatrix} 0\\ 2\\ 0 \end{pmatrix}\,.
\]
Ensuite, cherchons les composantes de \(\boldsymbol{x}\)
relativement à \(\mathcal{B}\), en utilisant le formalisme présenté plus haut.
Pour bien faire, récrivons explicitement ce que nous savons:
\[ [\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}\,, \]
ainsi que
\[
[\boldsymbol{b}_1]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}\,,\qquad
[\boldsymbol{b}_2]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix}\,,\qquad
[\boldsymbol{b}_3]_{\mathcal{B}_{\mathrm{can}}}= \begin{pmatrix} 0\\ 2\\ 0 \end{pmatrix}\,.
\]
Pour exprimer les composantes de \(\boldsymbol{x}\)
relativement à \(\mathcal{B}\), nous allons utiliser la formule
\[
[\boldsymbol{x}]_\mathcal{B}=P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}\,,
\]
où la matrice de changement de base est donnée par
\[ P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}=
\bigl[
[\boldsymbol{e}_1]_{\mathcal{B}}\, [\boldsymbol{e}_1]_{\mathcal{B}}\, [\boldsymbol{e}_1]_{\mathcal{B}} \bigr]\,.
\]
Or si on écrit explicitement les définitions des vecteurs de la base \(\mathcal{B}\),
\[
\left\{
\begin{array}{ccccc}
\boldsymbol{b}_1 &=&&& \boldsymbol{e}_3\\
\boldsymbol{b}_2 &=&\boldsymbol{e}_1&&-\boldsymbol{e}_3 \\
\boldsymbol{b}_3 &=&&2\boldsymbol{e}_2&
\end{array}
\right.
\]
Comme on doit exprimer les composantes des vecteurs de la base canonique par
rapport à \(\mathcal{B}\), il faut inverser ces relations. On trouve facilement
\[
\left\{
\begin{array}{ccccc}
\boldsymbol{e}_1 &=&\boldsymbol{b}_1&+\boldsymbol{b_2}&\\
\boldsymbol{e}_2 &=&&&\frac12 \boldsymbol{b}_3 \\
\boldsymbol{e}_3 &=&\boldsymbol{b}_1&&
\end{array}
\right.\,,
\]
c'est-à-dire
\[
[\boldsymbol{e}_1]_{\mathcal{B}}= \begin{pmatrix}1 \\1 \\0 \end{pmatrix}\,,\qquad
[\boldsymbol{e}_2]_{\mathcal{B}}= \begin{pmatrix}0 \\0 \\ \frac12 \end{pmatrix}\,,\qquad
[\boldsymbol{e}_3]_{\mathcal{B}}= \begin{pmatrix}1 \\0 \\0 \end{pmatrix}\,,
\]
qui donne
\[\begin{aligned}
[\boldsymbol{x}]_\mathcal{B}
&=P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}[\boldsymbol{x}]_{\mathcal{B}_{\mathrm{can}}}\\
&=
\begin{pmatrix}
1&0&1\\
1&0&0\\
0&\frac12&0
\end{pmatrix}
\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}\\
&=
\begin{pmatrix} 4\\ 1\\ 1 \end{pmatrix}\,.
\end{aligned}\]
Remarque:
Pour le calcul de \(P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}\), une façon tout à fait
équivalente de faire mais écrite différemment
aurait été de commencer par calculer
\[
P_{\mathcal{B}_{\mathrm{can}}\mathcal{B}}=
\bigl[
[\boldsymbol{b}_1]_{\mathcal{B}_{\mathrm{can}}}\, [\boldsymbol{b}_2]_{\mathcal{B}_{\mathrm{can}}}\, [\boldsymbol{b}_3]_{\mathcal{B}_{\mathrm{can}}} \bigr]
=
\begin{pmatrix}
0&1&0\\
0&0&2\\
1&-1&0
\end{pmatrix}\,,
\]
puis de calculer son inverse (par exemple avec l'algorithme de Gauss-Jordan):
\[
P_{\mathcal{B}\mathcal{B}_{\mathrm{can}}}=
{P_{\mathcal{B}_{\mathrm{can}}\mathcal{B}}}^{-1}=
\begin{pmatrix}
1&0&1\\
1&0&0\\
0&\frac12&0
\end{pmatrix}\,.
\]
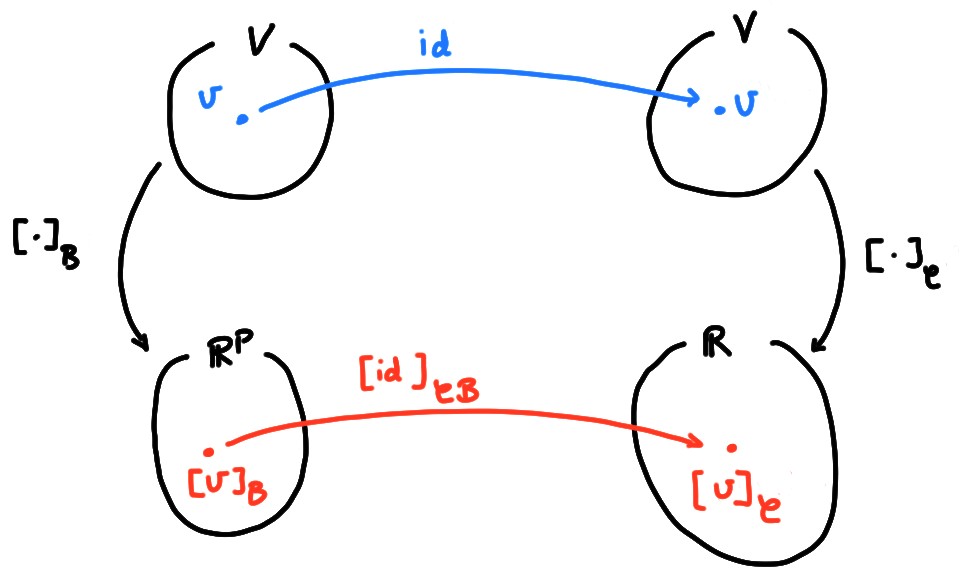
La matrice \(P_{\mathcal{C}\mathcal{B}}\) comme matrice d'une application
La matrice de changement de base peut être vue comme un cas particulier de
matrice associée à une application linéaire, introduite dans le chapitre sur les
espaces vectoriels.
En effet,
considérons l'application identité
\(\mathrm{id} :V\to V\), définie par
\[
\mathrm{id}(v):= v\qquad \forall v\in V\,.
\]
Cette application ne porte en elle rien de vraiment intéressant.
Mais considérons comme avant deux bases pour décrire \(V\), notées
\(\mathcal{C}\) et \(\mathcal{B}\).
Par définition, la matrice qui représente \(\mathrm{id}\)
relativement aux bases \(\mathcal{B}\) et \(\mathcal{C}\), est celle qui permet d'obtenir
\([v]_{\mathcal{C}}\) à partir de \([v]_{\mathcal{B}}\):
\[ [v]_{\mathcal{C}}=[\mathrm{id}]_{\mathcal{C}\mathcal{B}}[v]_{\mathcal{B}}.
\]
Cette matrice est donc précisément notre matrice de changement de base:
\[
P_{\mathcal{C}\mathcal{B}}=[\mathrm{id}]_{\mathcal{C}\mathcal{B}}\,.
\]