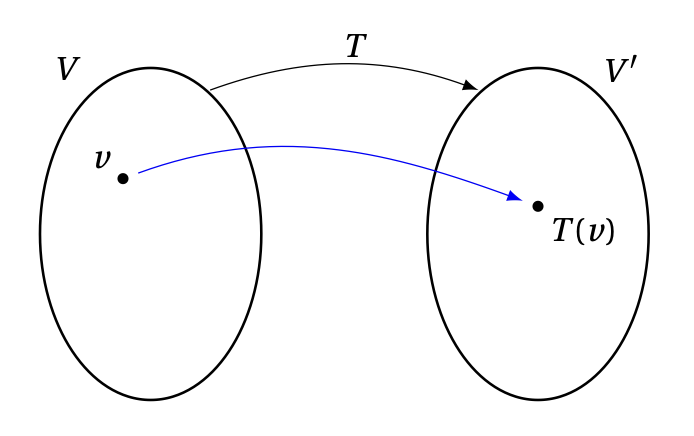
Dans cette section, nous généralisons la notion d'application linéaire, au cas d'une application d'un espace vectoriel \(V\) (de départ) dans un espace vectoriel \(V'\) (d'arrivée):
Étant des espaces vectoriels, \(V\) et \(V'\) possèdent chacun un zéro; on les notera \(\mathbf{0}_V\in V\) et \(\mathbf{0}_{V'}\in V'\) pour les distinguer. Par contre, l'addition dans ces espaces sera toujours notée ''\(+\)'' pour ne pas trop alourdir les notations .
Rappelons rapidement, dans ce cadre général, quelques notions élémentaires de la théorie des applications (ou fonctions) \(T:V\to V'\). Si nécessaire, on pourra aller voir ici , pour d'autres exemples à propos de ces notions. Pour tout \(V\), on notera \( \mathrm{id}_V : V \rightarrow V\) l'application identité de \(V\) qui associe \(v\) à tout \( v \in V\).
On rappelle que, étant donné deux applications \(T:V\to V'\) et \(S:V'\to V''\), la composition \( S\circ T \) est l'application définie par \[\begin{aligned} S\circ T:V&\to V'' \\ v&\mapsto (S\circ T)(v):= S\big(T(v)\big)\,. \end{aligned}\]
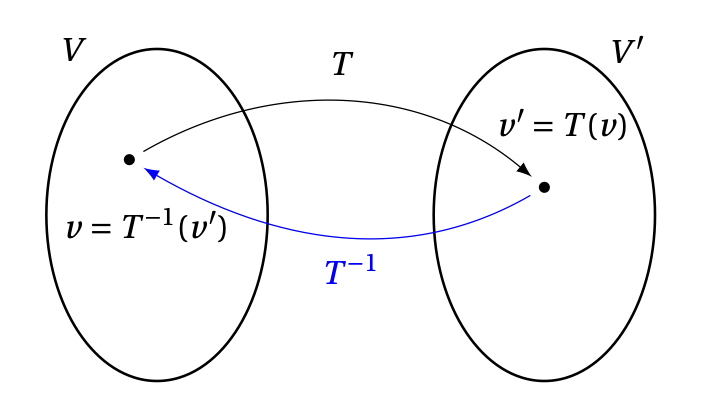
De façon graphique, on a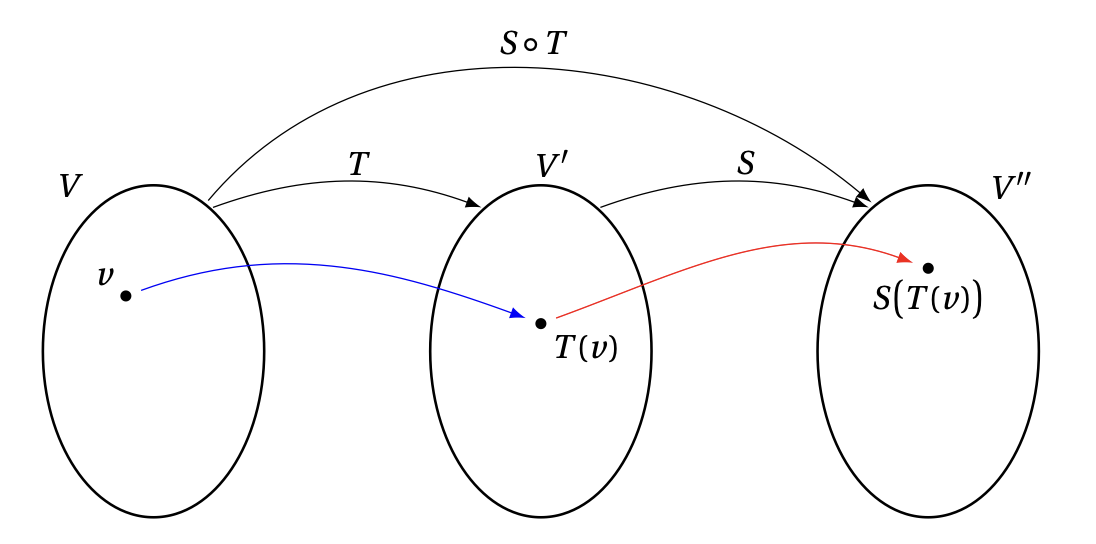
Rappelons que pour \(v\in V\), l'élément \(v'=T(v)\in V'\) est appelé l'image de \(v\), et \(v\) est une préimage de \(v'\). En outre,
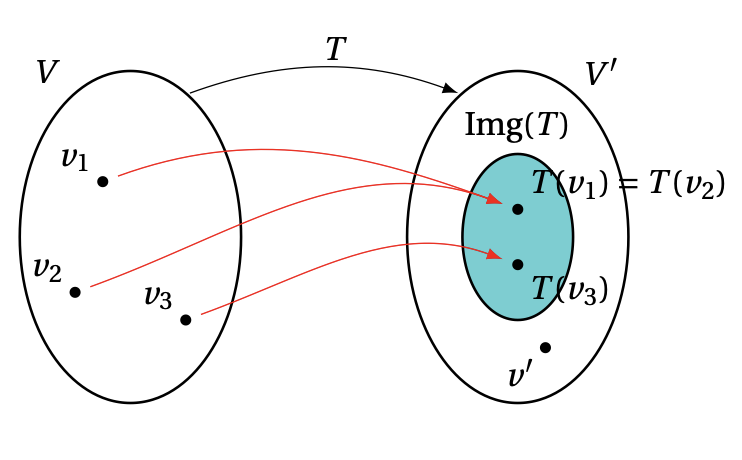
Remarquons que:
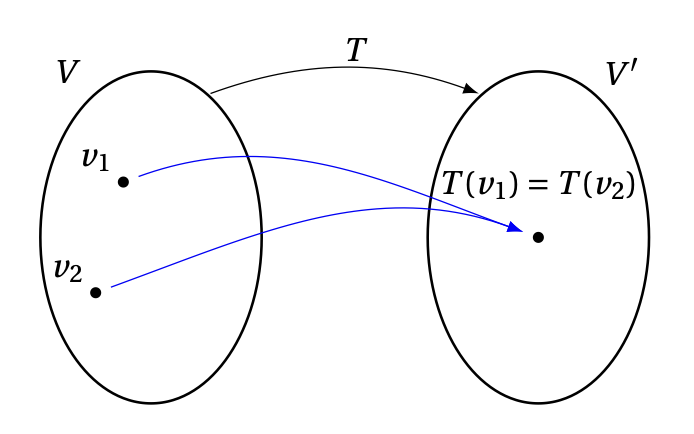
On voit que l'inversibilité et bijectivité d'une application sont en fait deux conditions équivalentes:
Lemme: Soit \( T : V \rightarrow V' \) une application. Alors les conditions suivantes sont équivalentes:
On suppose d'abord que \( T \) est bijective. Étant donné \(v'\in V'\), comme \(T\) est surjective, \(v'\) possède au moins une préimage: il existe un \(v_*\in V\) tel que \[ T(v_*)=v'\,. \] Mais comme \(T\) est aussi injective, il ne peut pas exister, à part \(v_*\), d'autre vecteur dont l'image soit égale à \(v'\). Par ce procédé, on associe à tout \(v'\in V'\) un unique \(v_*\in V\) tel que \(T(v_*)=v'\). On note \( S : V' \rightarrow V \) l'application qui à chaque \(v'\) associe son unique préimage \(v_*\). Par construction, on a \[\begin{aligned} T\big(S(v')\big)&=v'\,, \qquad \forall v'\in V'\,, \\ S\big(T(v)\big)&=v\,, \qquad \hskip 0.1cm \forall v\in V\,, \end{aligned}\] ce qui nous dit que \(T\) est inversible. Réciproquement, si \(T\) est inversible, soit \(S : V' \rightarrow V \) l'application inverse. Étant donné \(v' \in V'\) quelconque, l'identité \(T \circ S = \mathrm{id}_{V'}\) nous dit que \( T(S(v')) = v'\), ce qui implique que \(v' \in \mathrm{Im} (T)\). En conséquence, \(T\) est surjective. En outre, soient \(v_1,v_2 \in V\) tels que \(T(v_1) = T(v_2)\). L'identité \(S \circ T = \mathrm{id}_{V}\) nous dit que \[ v_1 = S\big(T(v_1)\big) = S\big(T(v_1)\big) = v_2, \] ce qui implique que \(T\) est injective. En conséquence, \(T\) est bijective.
Généralisons maintenant la notion d'application linéaire, que nous avions précédemment définie seulement dans le cas \(T:\mathbb{R}^n\to\mathbb{R}^m\):
Remarque: De même que dans première Remarque après la définition d'application linéaire dans la Section (cliquer), la linéarité implique que le vecteur nul est toujours envoyé sur le vecteur nul: \[ T(\mathbf{0}_{V})=\mathbf{0}_{V'}\,. \] En effet, en écrivant \(\mathbf{0}_{V}=\mathbf{0}_{V}+ 1.\mathbf{0}_{V}\) et en utilisant la linéarité, \[ T(\mathbf{0}_{V})=T(\mathbf{0}_{V}+1.\mathbf{0}_{V})=T(\mathbf{0}_{V})+1.T(\mathbf{0}_{V})=T(\mathbf{0}_{V})+T(\mathbf{0}_{V})\,. \] Si l'on somme à chaque membre \(-T(\mathbf{0}_{V})\) on trouve bien que \(T(\mathbf{0}_{V})=\mathbf{0}_{V'}\).
Remarque: On remarque qu'une application \(T:V\to V'\) est linéaire si et seulement si les deux conditions suivantes sont satisfaites:
Nous avons déjà vu plusieurs exemples d'applications linéaires dans le cas \(T:\mathbb{R}^n\to\mathbb{R}^m\). Rappelons le plus important:
Exemple: Si \(A\) est une matrice réelle \(m\times n\), alors l'application \[\begin{aligned} T:\mathbb{R}^n&\to\mathbb{R}^m \\ \boldsymbol{x}&\mapsto T(\boldsymbol{x}):= A\boldsymbol{x} \end{aligned}\] est linéaire.
Exemple: Soit \(V\) l'espace des fonctions \(f:[a,b]\to \mathbb{R}\), soit \(V'=\mathbb{R}^2\), et soit \(T:V\to V'\) définie ainsi: pour tout \(f\in V\), \[ T(f):= \begin{pmatrix} f(a)\\ f(b) \end{pmatrix}\,. \] Alors \(T\) est linéaire. En effet, si \(f,g\in V\), \(\alpha,\beta\in\mathbb{R}\), alors \[\begin{aligned} T(f+\lambda g) &= \begin{pmatrix} (f+\lambda g)(a)\\ (f+\lambda g)(b) \end{pmatrix} = \begin{pmatrix} f(a)+\lambda g(a)\\ f(b)+\lambda g(b) \end{pmatrix}\\ &= \begin{pmatrix} f(a)\\ f(b)\end{pmatrix}+ \lambda \begin{pmatrix} g(a)\\ g(b)\end{pmatrix} = T(f)+\lambda T(g)\,. \end{aligned}\]
Exemple: Soit \(V=C([a,b])\) l'espace des fonctions (à valeurs réelles) continues sur \([a,b]\), et soit \(V'=\mathbb{R}^2\). Soit \(c\in \hskip 0.6mm ]a,b[\) un point fixé et soit \(T:V\to V'\) définie ainsi: pour tout \(f\in V\), \[ T(f):= \begin{pmatrix} \displaystyle \int_a^c f(t)\,dt\\ \displaystyle \int_c^b f(t)\,dt \end{pmatrix}\,. \] Alors \(T\) est linéaire et surjective. (voir exercices)
Lemme: Soient \(T:V\to V'\) et \(S:V'\to V''\) des applications linéaires.
Pour démontrer que la composition \(S \circ T : T \to V''\) est une application linéaire, on note que \[ (S \circ T)(v_1 + \lambda v_2) = S \big(T(v_1 + \lambda v_2)\big) = S \big(T(v_1) + \lambda T(v_2)\big) = S \big(T(v_1)\big) + \lambda S \big(T(v_2)\big) = (S \circ T)(v_1) + \lambda (S \circ T)(v_2), \] pour tous \(v_1, v_2 \in V\) et \(\lambda \in \mathbb{R}\), où l'on a utilisé dans la deuxième égalité que \(T\) est une application linéaire et dans la troisième égalité que \(S\) est une application linéaire. On va montrer que si \(T\) est bijective alors \(T^{-1}:V'\to V\) est aussi linéaire. Or, pour \(v'_1, v'_2 \in V'\) et \(\lambda \in \mathbb{R}\), on a \[ T \big(T^{-1}(v'_1) + \lambda T^{-1} T(v'_2)\big) = T \big(T^{-1}(v'_1)\big) + \lambda T \big(T^{-1}(v'_2)\big) = v'_1 + \lambda v'_2 = T \big(T^{-1}(v'_1 + \lambda v'_2)\big), \] où l'on a utilisé que \(T\) est une application linéaire dans la première égalité, et que \(T\) et \(T^{-1}\) sont des applications réciproques dans la deuxième et dernière égalités. On rappelle que l'injectivité de \(T\) veut dire que \(T(v_1) = T(v_2)\) pour \(v_1, v_2 \in V\) implique \(v_1 = v_2\). En conséquence, l'identité démontrée et l'injectivité de \(T\) impliquent que \[ T^{-1}(v'_1) + \lambda T^{-1} (v'_2) = T^{-1}(v'_1 + \lambda v'_2), \] comme on voulait prouver.
Lorsqu'une application \(T:V\to V'\) est linéaire, plusieurs choses peuvent être
dites à son sujet.
Comme \( \mathbf{0}_{V} \) est toujours envoyé sur \(\mathbf{0}_{V'}\), il se pourrait aussi que d'autres
éléments de \(V\) soient aussi envoyés sur \(\mathbf{0}_{V'}\):
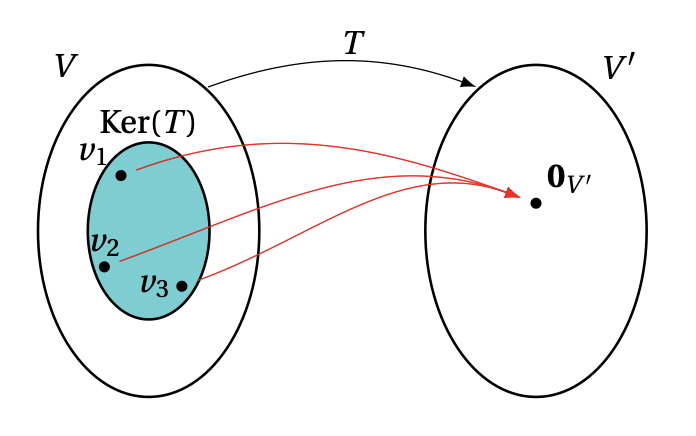
On a vu plus haut que le noyau contient toujours le zéro de \(V\). On peut en dire un peu plus:
Lemme: Une application linéaire \(T:V\to V'\) est injective si et seulement si son noyau ne contient que le zéro: \(\mathrm{Ker}(T)=\{\mathbf{0}_{V'}\}\).
Supposons d'abord que \(T\) est injective.
Considérons un \(v\in \mathrm{Ker}(T)\), c'est-à-dire tel que
\(T(v)=\mathbf{0}_{V'}\). Comme on sait que \(T(\mathbf{0}_{V})=\mathbf{0}_{V'}\), on a donc
\(T(v)=T(\mathbf{0}_{V})\), et l'injectivité implique que \(v=\mathbf{0}_{V}\). Donc
\(\mathrm{Ker}(T)=\{\mathbf{0}_{V}\}\).
Supposons maintenant que \(\mathrm{Ker}(T)=\{\mathbf{0}_{V'}\}\).
Considérons \(v_1,v_2\in V\) tels que \(T(v_1)=T(v_2)\). Par linéarité, ceci
implique \(T(v_1-v_2)=\mathbf{0}_{V'}\), et donc \(v_1-v_2\in \mathrm{Ker}(T)\), et donc
\(v_1-v_2=\mathbf{0}_{V}\), ce qui implique \(v_1=v_2\). Donc \(T\) est injective.
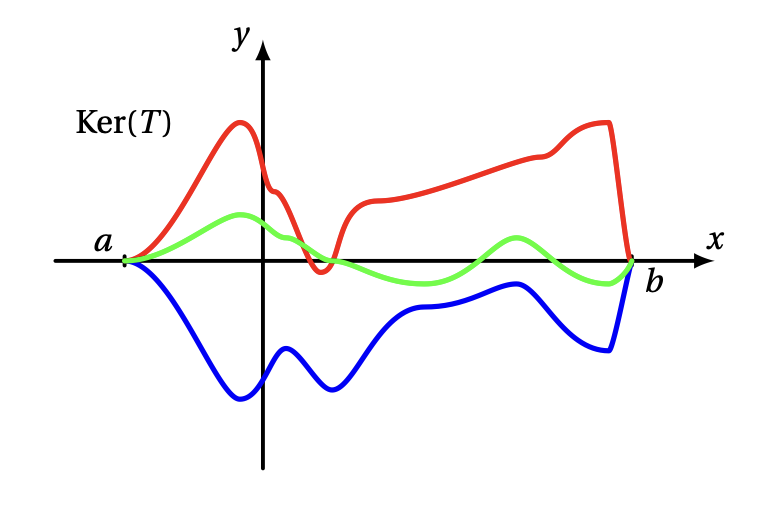
Exemple: Soit \(T:V\to \mathbb{R}^2\) l'application linéaire définie plus haut; pour \(f:[a,b]\to\mathbb{R}\), \[ T(f):= \begin{pmatrix} f(a)\\ f(b) \end{pmatrix}\,. \] Le noyau de cette application est formé de toutes les fonctions \(f\) pour lesquelles \[ T(f)=\boldsymbol{0}= \begin{pmatrix} 0\\ 0 \end{pmatrix}\,, \] c'est-à-dire \[ \mathrm{Ker}(T)=\big\{f:[a,b]\to \mathbb{R}\,:\,f(a)=f(b)=0\big\}\,. \] Ce noyau contient en particulier la fonction identiquement nulle bien-sûr, mais aussi une infinité de fonctions non-nulles:
Finalement, notons que le noyau et l'image sont des sous-ensembles stables de \(V\) et \(V'\), respectivement:
On a vu que \(T(\mathbf{0}_{V})=\mathbf{0}_{V'}\) (voir la première Remarque après la Définition d'application linéaire dans cette section), ce qui signifie que \(\mathbf{0}_{V}\in \mathrm{Ker}(T)\) et \(\mathbf{0}_{V'}\in \mathrm{Im} (T)\). Pour montrer que \(\mathrm{Ker}(T)\) est un sous-espace vectoriel de \(V\), étant donné \(v_1,v_2\in \mathrm{Ker}(T)\) et \(\lambda \in \mathbb{R}\), alors la linéarité de \(T\) implique \[ T(v_1+\lambda v_2)=\underbrace{T(v_1)}_{=\mathbf{0}_{V'}} +\lambda \underbrace{T(v_2)}_{=\mathbf{0}_{V'}}=\mathbf{0}_{V'}\,, \] et donc \(v_1+\lambda v_2\in \mathrm{Ker}(T)\). Pour montrer que \(\mathrm{Im} (T)\) est un sous-espace vectoriel de \(V'\), étant donné \(w_1,w_2\in \mathrm{Im} (T)\) et \(\lambda \in \mathbb{R}\), il suffit de montrer que \(w_1+\lambda W_2\in \mathrm{Im} (T)\). Or, la définition d'image nous dit qu'il existe \(v_1,v_2\in V\) tels que \(w_1 = T(v_1)\) et \(w_2 = T(v_2)\). La linéarité de \(T\) implique \[ w_1 + \lambda w_2 = T(v_1)+\lambda T(v_2) = T(v_1 +\lambda v_2) \in \mathrm{Im} (T)\,, \] comme on voulait démontrer.
Dernière compilation: 2025-09-02 (09:33:29)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
