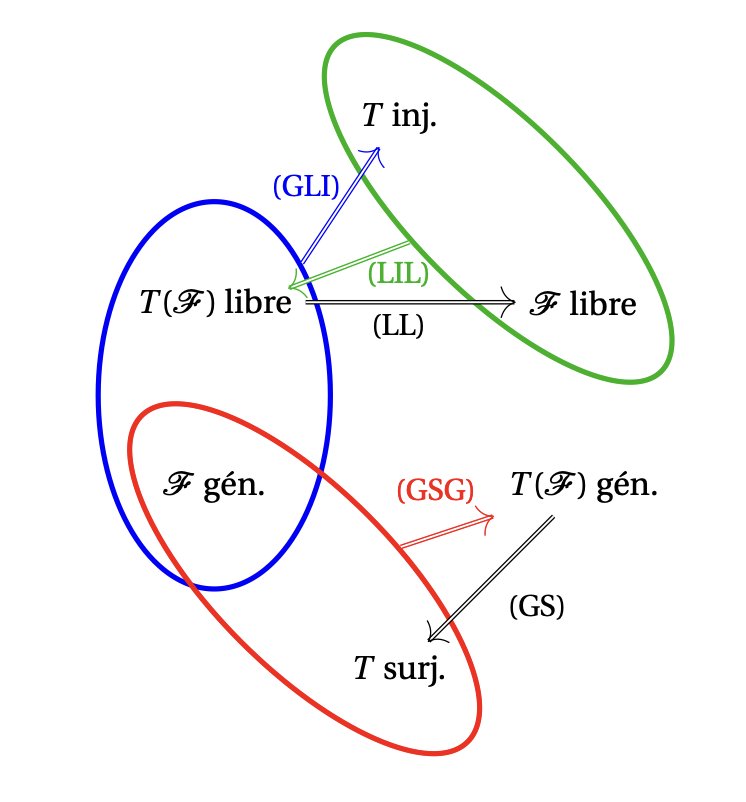
Théorème: Soit \(T:V\to V'\) une application linéaire et soit \( \mathcal{F} = \{ v_1, \dots, v_r \} \subseteq V\) une famille. On rappelle que \( T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est la famille image.
On montre d'abord l'implication (LL). On suppose que \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est libre. Considérons une combinaison linéaire nulle des éléments de \(\mathcal{F}\) donnée par \[ \mathbf{0}_{V} = \alpha_1 v_1+\cdots+\alpha_r v_r. \] Alors, la linéarité de \(T\) nous dit que \[ \mathbf{0}_{V'} = T(\mathbf{0}_{V'}) = T(\alpha_1 v_1+\cdots+\alpha_r v_r) = \alpha_1 T(v_1)+\cdots+\alpha_r T(v_r). \] Comme \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est libre, on déduit que \(\alpha_1=\dots=\alpha_r=0\), i.e. \(\mathcal{F}\) est libre. On prouve ensuite l'implication (LL). On suppose que \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est une famille génératrice de \(V'\). Alors, pour tout \(v' \in V'\) il existe \(\alpha_1 , \dots, \alpha_r \in \mathbb{R}\) tels que \[ v' = \alpha_1 T(v_1)+\cdots+\alpha_r T(v_r) = T(\alpha_1 v_1+\cdots+\alpha_r v_r), \] où l'on a utilisé la linéarité de \(T\) dans la dernière égalité. En conséquence, \(v' \in \mathrm{Im} (T)\), ce qui nous dit que \(T\) est surjective. On montre maintenant l'implication (LIL). On suppose que \(T\) est une application linéaire injective, et on va montrer que \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est libre. Considérons une combinaison linéaire nulle des éléments de \(T(\mathcal{F})\), \[ \mathbf{0}_{V'}=\alpha_1 T(v_1)+\cdots +\alpha_r T(v_r)=T(\alpha_1 v_1+\cdots +\alpha_r v_r)\,. \] Comme \(T\) est injective, on a \(\alpha_1v_1+\cdots +\alpha_r v_r=\mathbf{0}_{V}\), et comme \(\mathcal{F}\) est une libre, on en déduit que \(\alpha_1=\dots=\alpha_r=0\), i.e. \(T(\mathcal{F})\) est libre. On prouve puis l'implication (GLI). On suppose que \( \mathcal{F} = \{ v_1, \dots, v_r \} \subseteq V\) est une famille génératrice de \(V\) et \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est libre. On va montrer que \(T\) est injective. Soient \(v, w \in V\) tels que \(T(v) = T(w)\). Alors, comme \( \mathcal{F}\) est une famille génératrice de \(V\), il existe \(\alpha_1 , \beta_1 \dots, \alpha_r, \beta_r \in \mathbb{R}\) tels que \[ v = \alpha_1 v_1+\cdots+\alpha_r v_r \qquad \text{ et } \qquad w = \beta_1 v_1+\cdots+\beta_r v_r. \] Or, \(T(v) = T(w)\) nous dit que \[ \alpha_1 T(v_1)+\cdots+\alpha_r T(v_r) = T(\alpha_1 v_1+\cdots+\alpha_r v_r) = T(v) = T(w) = T(\beta_1 v_1+\cdots+\beta_r v_r) = \beta_1 T(v_1)+\cdots+\beta_r T(v_r), \] ce qui implique que \[ (\alpha_1 - \beta_1) T(v_1)+\cdots+ (\alpha_r - \beta_r)T(v_r) = \mathbf{0}_{V'}. \] Comme \(T(\mathcal{F})\) est libre, on conclut que \(\alpha_1 - \beta_1 = 0\), \dots, \(\alpha_r - \beta_r = 0\), i.e. \(\alpha_1 = \beta_1\), \dots, \(\alpha_r = \beta_r\), ce qui implique \[ v = \alpha_1 v_1+\cdots+\alpha_r v_r = \beta_1 v_1+\cdots+\beta_r v_r = w. \] En conséquence, \(T\) est injective. On montre l'implication dans (GSG). On suppose que \( \mathcal{F} = \{ v_1, \dots, v_r \} \subseteq V\) est une famille génératrice de \(V\) et \(T\) est surjective. On va montrer que \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est une famille génératrice de \(V'\). Soit \( v' \in V'\). Comme \(T\) est surjective, il existe \( v \in V\) tel que \(T(v) = v'\). Comme \( \mathcal{F} = \{ v_1, \dots, v_r \} \subseteq V\) est une famille génératrice de \(V\), il existe \(\alpha_1 , \dots, \alpha_r \in \mathbb{R}\) tels que \[ v = \alpha_1 v_1+\cdots+\alpha_r v_r. \] En conséquence, \[ v' = T(v) = T(\alpha_1 v_1+\cdots+\alpha_r v_r) = \alpha_1 T(v_1)+\cdots+\alpha_r T(v_r), \] ce qui implique que \(v' \in \mathrm{Vect}{T(\mathcal{F})}\), i.e. \(T(\mathcal{F}) = \{ T(v_1), \dots, T(v_r) \} \subseteq V'\) est une famille génératrice de \(V'\). Finalement, pour prouver la dernière partie, on note que si \(T\) est bijective et \(\mathcal{B}=\{v_1,\dots,v_p\}\) une base de \(V\), alors (LIL) et (GSG) nous disent que \(T(\mathcal{B})=\{T(v_1),\dots,T(v_p)\}\) est une base de \(V'\). Réciproquement, étant donné une base \(\mathcal{B}=\{v_1,\dots,v_p\}\) de \(V\), si \(T(\mathcal{B})=\{T(v_1),\dots,T(v_p)\}\) est une base de \(V'\), (GLI) et (GS) nous disent que \(T\) est bijective.
On peut résumer toutes les implications du Théorème précédent de la forme graphique suivante:
