Même si elle est élémentaire, la définition
de supremum/infimum (voir
ici)
nécessite de travailler avec un nombre arbitrairement petit
(un ''\(\forall\)''), des inégalités...
Cet exercice a pour but d'entraîner l'intuition en trouvant des
supremums/infimums,
uniquement en se souvenant de leurs définitions de base et les visualisant:
le supremum est le plus petit majorant, l'infimum est le plus grand minorant.
Pour la plupart, les ensembles considérés peuvent être
représentés facilement sur la droite, donc on pourra faire
un simple croquis pour comprendre à quoi ils ressemblent.
On a \(\inf B = \sqrt{3}\notin B\) et \(\sup B = +\infty\) puisque \(B\) n'est
pas majoré.
\(B\) n'admet ni minimum ni maximum.
\(C=\{x\in\mathbb{R}: -1\leqslant 2x-1\leqslant 1 \}=[0,1]\). Ainsi
\(\inf C = \min C=0\) et \(\sup C = \max C = 1\).
\(D= \{x\in\mathbb{R}: -1\lt x^2-2\lt 1 \}=]-\sqrt{3},-1\,[\:\cup\:]\,1,
\sqrt{3}\,[\).
Ainsi
\(\inf D = -\sqrt{3}\) et \(\sup D = \sqrt{3}\) qui ne sont pas
minimum et maximum car pas dans \(D\).
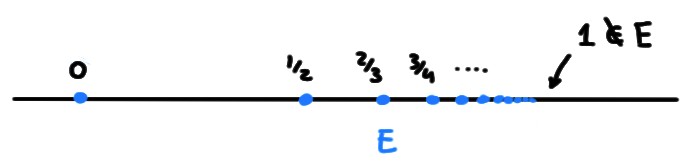
Remarquons que
\(E = \{ 0, \frac{1}{2}, \frac{2}{3},\frac{3}{4},\ldots\}
=\{1-\frac{1}{n+1}: n\in\mathbb{N}\}\).
Ainsi \(\inf E = 1 - \frac{1}{0+1}=0=\min E\) et \(\sup E = 1\).
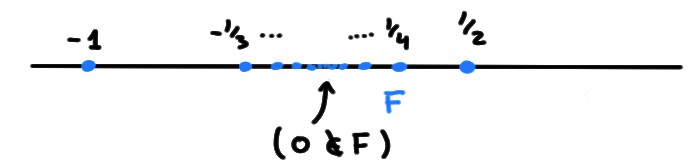
Puisque
\[\begin{aligned}
F&=\bigl\{-1,\tfrac12,-\tfrac13,
\tfrac14,\dots\bigr\}\\
&=
\bigl\{-1,-\tfrac13,-\tfrac15,\dots\}
\cup\{\tfrac12,\tfrac14,\tfrac16,\dots\bigr\}\,,
\end{aligned}\]
on a \(\inf F=\min F=-1\) et
\(\sup F=\max F=\frac12\).
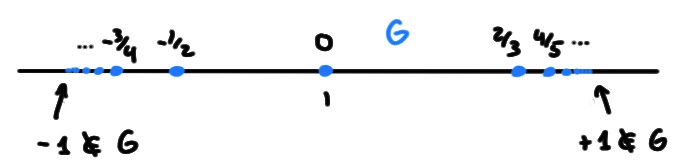
On a
\[G=\bigl\{0,-\tfrac{1}{2},\tfrac{2}{3},-\tfrac{3}{4},\ldots\bigr\}\,.\]
Ainsi \(\inf G = -1\) et
\(\sup G = 1\).
Comme \(-1,1\notin G\), \(G\) n'a pas de minimum ni de maximum.
Comme \(\mathbb{Q}\) n'est ni minoré ni majoré, on a \(\inf H = -\infty\) et
\(\sup H=+\infty\). \(H\) n'a bien-sûr pas de minimum, ni de maximum.
D'une part, \(\inf I=0\). En effet, \(0\) minore \(I\), et
pour tout \(\varepsilon\gt 0\), il existe
un entier \(n\) tel que \(0\lt \frac{1}{n}\lt \varepsilon\). Comme \(\frac{1}{n}\in
I\), ceci montre que \(0\) est bien l'infimum.
D'autre part, \(\sup I=1\).
En effet, \(1\) majore \(I\). De plus, pour tout \(\varepsilon\gt 0\) il existe un
entier \(n\gt 1\) tel que \(0\lt \frac{1}{n}\lt \varepsilon\), et donc tel que
\(1-\varepsilon\lt 1-\frac{1}{n}\lt 1\). Puisque \(1-\frac{1}{n}=\frac{n-1}{n}\in
\mathbb{Q}\), ceci montre que \(1-\varepsilon\) ne majore pas \(I\). Donc
\(\sup I\) est bien égal à \(1\).
Remarquons que \(I\) ne possède ni minimum ni maximum.