Exercice 13-03
Soit \(f:\mathbb{R}\to \mathbb{R}\) définie par \[ f(x):= \begin{cases} e^{-\frac{1}{x^2}}&\text{ si }x\neq 0\,,\\ 0&\text{ si }x=0\,. \end{cases} \]
  1. Montrer que \(f\in C^\infty(\mathbb{R})\).
  2. Calculer la série de MacLaurin de \(f\) (en \(x_0=0\)), ainsi que son rayon de convergence.
  3. Que concluez vous?
Cet exercice a pour but de montrer qu'il ne suffit pas qu'une fonction soit \(C^\infty\) pour qu'elle soit entièrement décrite par sa série de Taylor.

Commencer par montrer, par récurrence sur \(n\geqslant 1\), que pour tout \(x\neq 0\), \(f^{(n)}(x)\) est de la forme \(p_n(1/x)e^{-1/x^2}\), où \(p_n(t)\) est un polynôme en \(t\).

Ensuite, étudier les dérivées de \(f\) en \(x=0\), en montrant par récurrence sur \(n\) que \(f^{(n)}(0)=0\) pour tout \(n\).

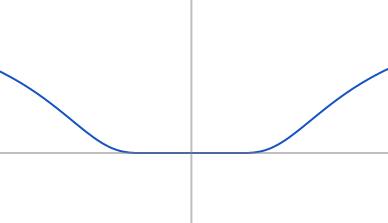
  1. Si \(x\neq 0\), alors \[f'(x) =\left(\frac{-1}{x^2}\right)'e^{-1/x^2} =\left(\frac{2}{x^3}\right)e^{-1/x^2} =p_1(1/x)e^{-1/x^2}\,, \] où \(p_1(t)=2t^3\). Supposons donc que pour un entier positif \(n\) donné, la \(n\)-ème dérivée de \(f\) peut s'écrire, en tout point \(x\neq 0\), sous la forme suivante: \[ f^{(n)}(x)=p_n(1/x)e^{-1/x^2}\,, \] où \(p_n(t)\) est un polynôme. Ceci implique en particulier que \(f^{(n)}\) est dérivable, et que \[ f^{(n+1)}(x) =(f^{(n)})'(x) =\underbrace{\left\{ p_n'(\frac1x)\left(\frac{-1}{x^2}\right)+p_n(\frac1x) \left(\frac{-1}{x^2}\right)' \right\}}_{=p_{n+1}(\frac1x)}e^{-1/x^2} \] Étudions maintenant les dérivées de \(f\) en \(0\). Pour la première, \[ f'(0)= \lim_{x\to 0}\frac{f(x)-0}{x-0}= \lim_{x\to 0}\frac{e^{-1/x^2}}{x}= \lim_{y\to \pm\infty}\frac{y}{e^{y^2}}=0\,. \] (On a fait le changement de variable \(y=1/x\). La limite \(x\to 0\) se sépare alors en deux limites latérales \(x\to 0^\pm\), qui correspondent à deux limites \(y\to \pm \infty\), que l'on a calculé en une seule fois puisqu'elles sont égales.)

    Par récurrence: supposons que \(f^{(n)}(0)=0\), et calculons \(f^{(n+1)}(0)\), en utilisant la représentation de \(f^{(n)}(x)\) obtenue plus haut, \[\begin{aligned} f^{(n+1)}(0)=(f^{(n)})'(0)&= \lim_{x\to 0} \frac{f^{(n)}(x)-0}{x-0}\\ &= \lim_{x\to 0} \frac{p_n(1/x)}{x}e^{-1/x^2}\\ &=\lim_{y\to \pm \infty} \frac{yp_n(y)}{e^{y^2}}=0\,. \end{aligned}\] Dans la dernière ligne, on a encore une fois posé \(y=1/x\) et utilisé le fait que \(e^{y^2}\) diverge plus vite que n'importe quel polynôme (démontré rigoureusement au cours à l'aide de la règle de BH).

    On a donc montré que toutes les dérivées \(f^{(n)}\) existent sur \(\mathbb{R}\), donc \(f\in C^\infty(\mathbb{R})\).
  2. Puisque \(f^{(k)}(0)=0\) pour tout \(k\), la série de MacLaurin de \(f\) est \[ \sum_{k\geqslant 0}\frac{f^{(k)}(0)}{k!}x^k =0+0x+0x^2+0x^4+\cdots \] Cette série converge pour tout \(x\), et donc son intervalle de convergence est tout \(\mathbb{R}\).
  3. Même si le développement de MacLaurin existe et converge partout, il ne décrit pas \(f\) (à part en \(x=0\)). En fait, si on considère le développement limité d'ordre \(n\) de \(f\) en \(x=0\), \[ f(x)=\underbrace{0+0\cdot x+\frac{0}{2!}x^2+\cdots +\frac{0}{n!}x^n}_{=0}+R_n(x)=R_n(x)\,. \] On conclut que le reste est égal à la fonction, pour tout \(x\), et ne dépend pas de \(n\). On a donc, pour tout \(x\neq 0\), que \[ \lim_{n\to\infty} R_n(x)\neq 0\,. \] \(f\) est donc une fonction dont la série de McLaurin existe (c'est la série dont tous les termes sont zéros, donc elle converge pour tout \(x\)), par contre cette série ne représente pas \(f\) au voisinage de zéro. C'est un exemple de fonction \(C^\infty\) qui ne peut pas être représentée par sa série de McLaurin.