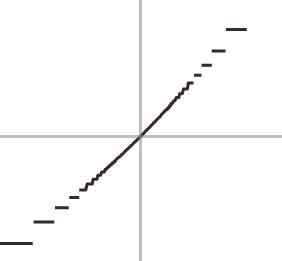
- Pour que \(f\) soit continue en \(x_0=0\), il faut que \[ \lim_{x\to 0}f(x)=f(0)=C\,. \] Pour étudier la limite du côté gauche, rappelons que \[ \frac1x -1 \leqslant \left\lfloor \frac{1}{x} \right\rfloor\leqslant \frac{1}{x} \qquad \forall x\,, \] ce qui donne \[ \frac{1}{\frac1x -1} \geqslant \frac{1}{\lfloor \frac{1}{x} \rfloor} \geqslant \frac{1}{\frac{1}{x}} \qquad \forall x\,, \] ou encore \[ x \leqslant \frac{1}{\lfloor \frac{1}{x} \rfloor} \leqslant \frac{x}{1-x} \qquad \forall x\,, \] Puisque \(\lim_{x\to 0}\frac{x}{1-x}=\lim_{x\to 0}x=0\), le théorème des deux gendarmes implique donc que \[ \lim_{x\to 0}f(x)=0 \] Donc l'unique valeur de \(C\) qui rend \(f\) continue en \(x_0=0\) est \(C=0\).
- Pour ensuite voir que \(f\) est dérivable en \(x_0=0\) lorsqu'on prend \(C=0\), on doit considérer la limite \[ \lim_{x\to 0}\frac{f(x)-f(0)}{x-0} = \lim_{x\to 0}\frac{1}{x\lfloor \frac1x \rfloor} \] Or si \(x\gt 0\), on peut réutiliser l'inégalité ci-dessus, pour écrire \[ 1-x\leqslant x\left\lfloor \frac1x \right\rfloor\leqslant 1 \qquad \forall x\gt 0\,, \] qui garantit \[ \lim_{x\to 0^+}\frac{1}{x\lfloor \frac1x \rfloor}=1\,. \] De même, si \(x\lt 0\), on peut réutiliser l'inégalité ci-dessus, pour écrire \[ 1-x\geqslant x\left\lfloor \frac1x \right\rfloor\geqslant 1 \qquad \forall x\lt 0\,, \] qui garantit \[ \lim_{x\to 0^-} \frac{1}{x\lfloor \frac1x \rfloor}=1\,. \] Ainsi, \(f\) est dérivable en \(x=0\), et \[ f'(0)= \lim_{x\to 0}\frac{f(x)-f(0)}{x-0} = \lim_{x\to 0}\frac{1}{x\lfloor \frac1x \rfloor} =1\,. \]