Exercice 08-07
Sans faire de calculs, donner les minimums et maximums, lorsqu'ils existent, des fonctions \(f:D\to \mathbb{R}\) ci-dessous.
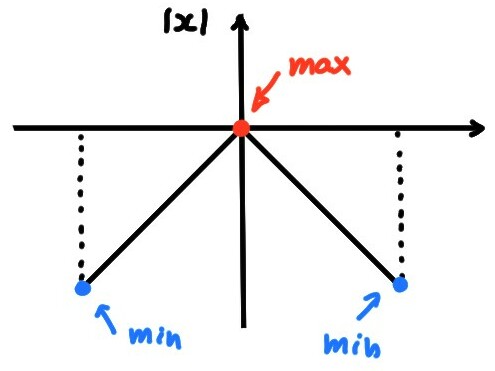
  1. \(D=[-1,1]\), \(f(x)=-|x|\)
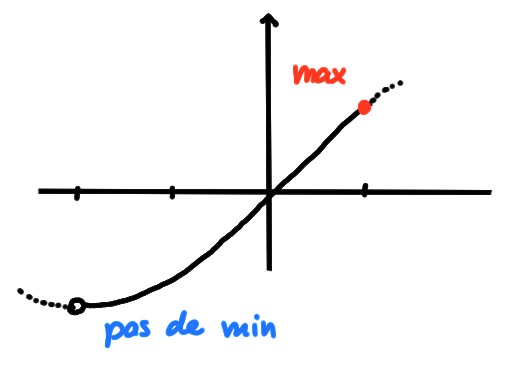
  2. \(D=]-\pi/2,\pi/4]\), \(f(x)=\sin(x)\)
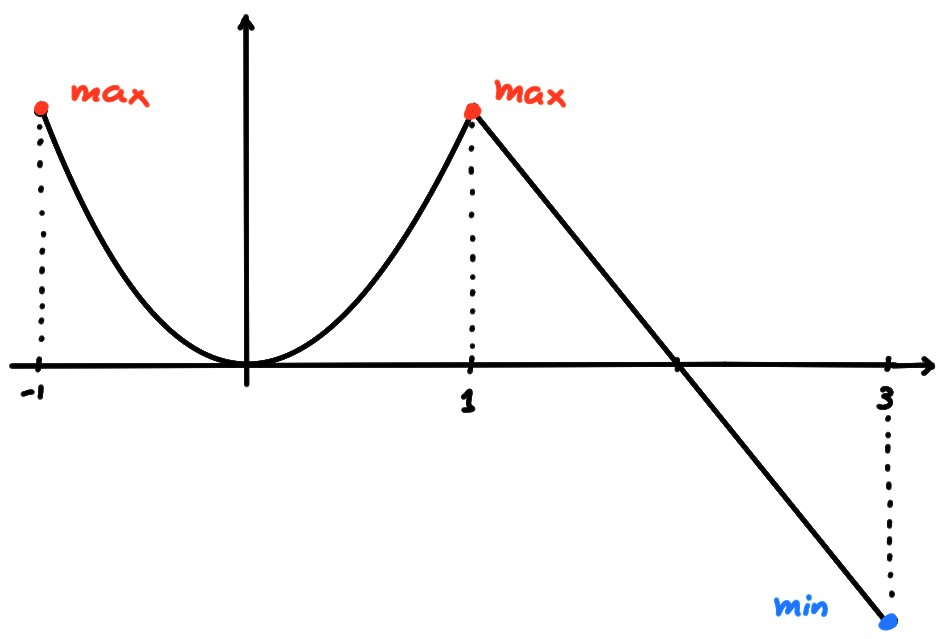
  3. \(D=[-1,3]\), \(f(x)= \begin{cases} x^2&-1\leqslant x\leqslant 1\,, \\ 2-x & 1< x\leqslant 3 \end{cases} \)
  4. \(D=\mathbb{R}\), \(f(x)= \begin{cases} \sin(1/x)&x\neq 0 \\ 0 & x=0 \end{cases} \)
  5. \(D=\mathbb{R}\), \(f(x)=\arctan(x)\)
Si un min/max existe, dire en quel(s) point(s) il est atteint.
On pourra sans autre faire un croquis pour étudier l'existence de points où un max/min est atteint.
  1. Maximum atteint en \(x^*=0\), minimum atteint en \(x_*=\pm 1\).
  2. Maximum atteint en \(x^*=\pi/4\), pas de minimum.
  3. Maximum atteint en \(x^*=\pm 1\), minimum en \(x_*=3\).
  4. Puisque \(\sin(y)\) est maximal (et vaut \(+1\)) lorsque \(y=\frac{\pi}{2}+2k\pi\), \(k\in \mathbb{Z}\), \(f(x)\) sera maximale lorsque \(\frac1x=\frac{\pi}{2}+2k\pi\), c'est-à-dire lorsque \(x\) est un point du type \[ x^*_k=\frac{1}{\frac{\pi}{2}+2k\pi}\,,\quad k\in \mathbb{Z}\,. \] (En particulier, \(f\) atteint son maximum en une infinité de points.) De même, \(f\) atteint son minimum (de valeur \(-1\)) en tous les points de la forme \[ x_{*,k}=\frac{1}{\frac{3\pi}{2}+2k\pi}\,,\quad k\in \mathbb{Z}\,. \]
  5. Pas de minimum, pas de maximum.