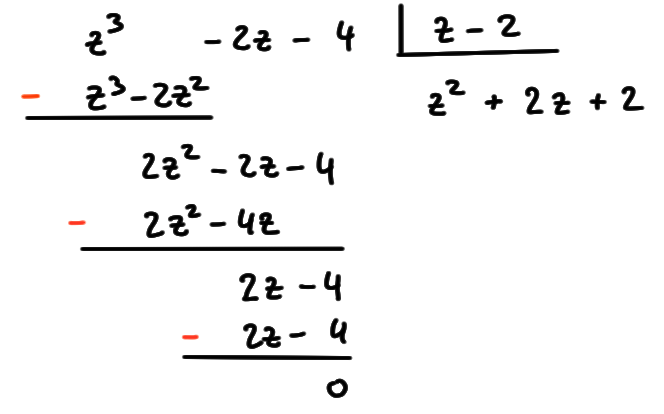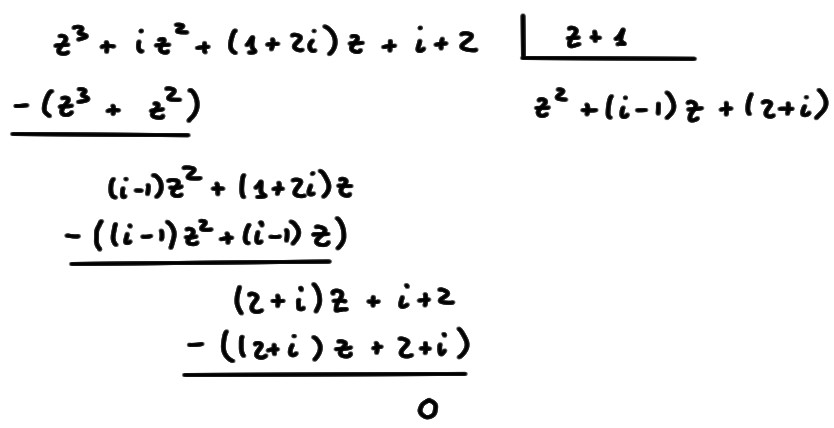Exercice 06-05
Factoriser les polynômes suivants:
  1. \(P(z)=z^3-2z-4\)
  2. \(P(z)=z^3+\mathsf{i} z^2+(1+2\mathsf{i})z+\mathsf{i}+2\).
  3. \(P(z)=1+z+z^2+z^3+\cdots+z^9+z^{10}\)
Le Théorème Fondamental de l'Algèbre garantit qu'un polynôme complexe \(P(z)\) peut toujours se factoriser en un produit de facteurs \((z-z_k)\), où les \(z_k\) sont les racines de \(P\). Mais réaliser concrètement cette factorisation dans un cas particulier requiert souvent un certain travail, parce que les racines on doit les calculer...

Donc ce qu'on fait, en pratique, c'est d'essayer de trouver des racines ''évidentes'', que l'on trouve simplement en testant des valeurs. En effet, en observant l'allure de \(P(z)\), il n'est pas exclu que l'on arrive à deviner un \(z_1\) tel que \(P(z_1)=0\). Ensuite, puisqu'on sait que \(P\) doit contenir \((z-z_1)\) dans sa factorisation, on sait que l'on a déjà \[ P(z)=(z-z_1)Q(z)\,. \] où \(Q(z)\) est degré strictement inférieur à celui de \(P(z)\). Puis on recommence avec \(Q\)...

On a vu des exemples ici.

Nous avons déjà vu ce genre de somme quelque part.

c'est une somme géométrique!

  1. Pour \(P(z)=z^3-2z-4\), on remarque que \(z_1=2\) est racine: \(P(2)=0\). On peut donc effectuer la division de \(P(z)\) par \(z-2\):
    Donc \[ P(z)=(z-2)Q(z)\,,\] où \(Q(z)=z^2+2z+2\). On a déjà factorisé ce polynôme au cours: \[ Q(z)=(z-(-1-\mathsf{i}))(z-(-1+\mathsf{i}))\,. \] On a donc \[ P(z)=(z-2)(z-(-1-\mathsf{i}))(z-(-1+\mathsf{i}))\,. \]
  2. On remarque que \(z_1=-1\) est racine: \(P(-1)=0\). On peut donc effectuer la division de \(P(z)\) par \(z-(-1)=z+1\):
    On a donc déjà que \[ P(z)=(z+1)Q(z)\,,\] où \(Q(z)=z^2+(\mathsf{i}-1)z+2+\mathsf{i}\). Puis, on recommence avec \(Q(z)=z^2+(\mathsf{i}-1)z+2+\mathsf{i}\): soit on calcule ses racines (comme avant), soit on remarque que \(Q\) s'annule en \(z=\mathsf{i}\). Donc on peut effectuer la division de \(Q(z)\) par \(z-\mathsf{i}\). Finalement, on trouve \[\begin{aligned} P(z)&=(z+1)Q(z)\\ &=(z+1)(z-\mathsf{i})(z-(1-2\mathsf{i})) \end{aligned}\]
  3. Remarquons que \(P\) ne s'annule pas en \(z=1\). On peut donc utiliser la formule \[ P(z)=1+z+z^2+z^3+\cdots+z^9+z^{10}=\frac{z^{10+1}-1}{z-1} \] Or on peut factoriser facilement \(z^{11}-1\), puisqu'on connaît les racines \(11\)-èmes de \(1\), qui sont \[ z_k=e^{\mathsf{i}\frac{2k\pi}{11}}\,\qquad k=0,1,2,\dots,10\,, \] et donc le théorème fondamental permet d'écrire \[ z^{11}-1=\prod_{k=0}^{10}(z-z_k)\,. \] Puisque \(z_0=1\), on a donc \[\begin{aligned} P(z)&=\prod_{k=1}^{10}(z-z_k)\\ &=(z-z_1)(z-z_2)\cdots (z-z_{10})\,. \end{aligned}\]