Exercice 06-02
Résoudre les équations suivantes dans \(\mathbb{C}\):
  1. \(z^{2}+6z+12-4\mathsf{i}=0\)
  2. \(z^{6}-2z^{3}+2=0\)
  3. \(\overline{z}^2=z+1\)
  4. \((\displaystyle\frac{z}{|z|})^3=\mathsf{i}\)
A priori, on peut s'attaquer à la résolution d'une équation du type \(f(z)=0\) de deux façons:
  1. En posant \(z=a+b\mathsf{i}\), et en décortiquant \(f(z)\) jusqu'à pouvoir mettre l'équation \(f(z)=0\) sous la forme \[ (\dots)+\mathsf{i}(\dots)=0\,, \] puis égaler les parties réelles et imaginaires de ce complexe à zéro, pour obtenir des conditions sur \(a\) et \(b\).
  2. En cherchant \(z\) sous forme polaire, \(z=re^{\mathsf{i} \theta}\), en décortiquant \(f(z)\) pour obtenir des conditions sur \(r\) et \(\theta\).

Commencer par poser \(u=z^3\), et résoudre l'équation en \(u\).

  1. Première méthode: On pose \(z=a+\mathsf{i} b\), et on injecte dans l'équation: \[(a+\mathsf{i} b)^2+6(a+\mathsf{i} b)+12-4\mathsf{i}=0\,, \] qui mène au système \[ \begin{cases} a^2 - b^2 + 6a + 12 & =0 \\ 2ab + 6b - 4 & =0\,. \end{cases} \] De la première équation on obtient \(a=-3\pm \sqrt{b^{2}-3}\), et donc \(|b|\geqslant\sqrt{3}\) car \(a\) doit être réel. On peut alors récrire la deuxième équation du système comme \(a=\frac{2}{b}-3\) et on trouve \[-3\pm\sqrt{b^2-3}=\frac{2}{b}-3 \,\Leftrightarrow \, \pm \sqrt{b^2-3}=\frac{2}{b}\,, \] d'où \(b^2-3=\frac{4}{b^2}\), ou encore \[ (b^2)^2-3b^2-4=(b^2-4)(b^2+1)=0\,. \] On a alors \(b=\pm 2\) car \(b\) doit être réel. Les solutions de l'équation initiale sont donc \(z_{1}=-2+2\mathsf{i}\), \(z_{2}=-4-2\mathsf{i}\).

    Deuxième méthode: On utilise directement la formule pour l'équation quadratique, \(az^2+bz+c=0\). Comme \(a=1\), \(b=6\) et \(c=12-4i\), on a \(\Delta=36-48+16\mathsf{i}=-12+16\mathsf{i}\). Pour utiliser la formule, qui dans le cas réel s'écrit ''\(\frac{-b\pm\sqrt{\Delta}}{2a}\)'', il nous faut donc calculer les racines carrées de \(-12+16\mathsf{i}=4(-3+4\mathsf{i})\). On a déjà calculé les racines carrées de \(-3+4\mathsf{i}\) dans un exercice précédent: \(\pm(1+2\mathsf{i})\). Les solutions de l'équation sont donc \[\begin{aligned} z_+&=\frac{-6+2(1+2\mathsf{i})}{2}=-2+2\mathsf{i}\,,\\ z_-&=\frac{-6-2(1+2\mathsf{i})}{2}=-4-2\mathsf{i}\,. \end{aligned}\]
  2. En posant \(z^3=w\), 'équation devient \(w^2-2w+2=0\), dont les solutions sont \(w=1\pm \mathsf{i}\). On cherche donc \[ z^{3}=1\pm \mathsf{i}=\sqrt{2}e^{\pm \mathsf{i}\frac{\pi}{4}}\,. \] Il faut alors résoudre les équations \[ z^3=\sqrt{2}e^{\mathsf{i}\frac{\pi}{4}}\, \quad \text{ et } z^3=\sqrt{2}e^{-\mathsf{i}\frac{\pi}{4}}\,, \] en utilisant la même technique qu'aux exercices précédents. On obtient \(6\) solutions: \[\begin{aligned} z_{1}&=\sqrt[6]{2}e^{i\frac{\pi}{12}}\,, z_{2}=\sqrt[6]{2}e^{i\frac{3\pi}{4}}\,, z_{3}=\sqrt[6]{2}e^{i\frac{17\pi}{12}}\\ z_{4}&=\sqrt[6]{2}e^{-i\frac{\pi}{12}}=\sqrt[6]{2}e^{i\frac{23\pi}{12}}\,, z_{5}=\sqrt[6]{2}e^{i\frac{7\pi}{12}}\,, z_{6}=\sqrt[6]{2}e^{i\frac{5\pi}{4}} \end{aligned}\]
  3. En posant \(z=a+b \mathsf{i}\), l'équation devient \[ \bigl(a^2-b^2-a-1\bigr)- b(2a+1)\mathsf{i}=0\,, \] on la résout en égalant les parties réelles et imaginaires à zéro. Si on regarde la partie imaginaire, celle-ci s'annule
    • si \(b=0\), qui injecté dans la partie réelle donne \(a^2-a-1=0\), qui possède deux solutions \(a=\frac{1\pm\sqrt{5}}{2}\), ou
    • si \(a=-\frac{1}{2}\), qui injecté dans la partie réelle donne \(b^2=-\frac{1}{4}\), qui n'a pas de solutions.
    L'équation de départ a donc deux solutions, réelles toutes les deux: \(z_\pm=\frac{1\pm\sqrt{5}}{2}\).
  4. Clairement, il faut exclure \(z=0\). On peut donc poser \(z=re^{i\theta}\) avec \(r>0\), et l'équation devient \[ \left(\frac{z}{|z|}\right)^3= (e^{\mathsf{i} \theta})^3= e^{\mathsf{i} 3\theta}=\mathsf{i}=e^{\mathsf{i}\frac{\pi}{2}}\,. \] On a donc \(3\theta=\frac{\pi}{2}+2k\pi\), ce qui donne \(3\) arguments possibles, \(\theta_k=\frac{\pi}{6}+k\frac{2\pi}{3}\), \(k=0,1,2\). Par contre, il n'y a aucune contrainte sur \(r>0\). L'équation possède donc une infinité de solutions, données par \[ \{re^{\mathsf{i} \theta_k}\,:\,r>0,\,k=0,1,2\}\,. 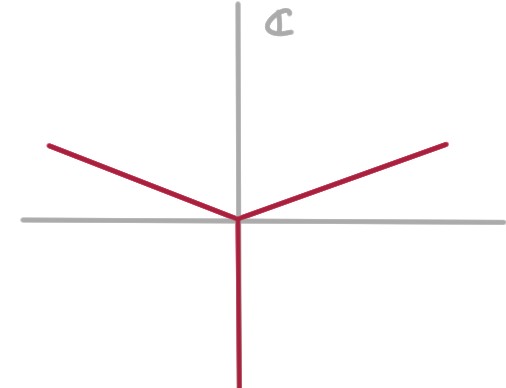\] Cet ensemble correspond à trois demi-droites partant de l'origine, faisant des angles de respectivement \(\theta_0=\frac{\pi}{6}\), \(\theta_1=\frac{5\pi}{6}\), et \(\theta_2=\frac{3\pi}{2}\) avec l'horizontale: